hier ein Link, wo sowas schonmal gemacht wurde.
https://mathelounge.de/551253/weglangenfunktion-der-folgenden-wege-berechnen
Ansonsten zum zweiten mal in Kurzform, weil die Stammfunktion davon zu finden schon eine harte Nuss ist.
Ansatz:
$$ L=\int_a^b\sqrt{x'(t)^2+y'(t)^2}dt\\f\Bigg(\begin{pmatrix}x(t)\\y(t) \end{pmatrix}\Bigg):=y(t)=\begin{pmatrix} t\\e^t \end{pmatrix}\\y'(t)=1\\y'(t)^2=e^{2t} $$ Eingesetzt ergibt:
$$ L=\int_0^1\sqrt{1+e^{2t}}dt=...\stackrel{(*)}{=}\Bigg[-\dfrac{\ln\left(\sqrt{\mathrm{e}^{2t}+1}+1\right)}{2}+\dfrac{\ln\left(\sqrt{\mathrm{e}^{2t}+1}-1\right)}{2}+\sqrt{\mathrm{e}^{2t}+1}\Bigg]_0^1\approx \underline{\underline{2.00350}} $$
(*) integralrechner.de
Numerische Herangehensweise
Falls dir das zu heftig sein sollte, bzw. ihr auch numerisch rangehen dürft, kannst du auch zum Beispiel die Trapezmethode verwenden, um dich so deinem Integral zu nähern.
1. WEG
$$ \int_a^bf(x)dx\approx\frac{f(a)+f(b)}{2}\cdot \frac{b-a}{n}+ \frac{b-a}{n}\cdot\sum_{k=1}^{n-1}{f\Big(a+k\cdot\frac{b-a}{n}\Big)} $$
a : Untergrenze, hier 0
b : Obergrenze, hier 1
n : äquidistante Zerlegung des Intervalls, hier [0,1] mit n=4
Dann hat man also:
$$ L=\int_0^1\sqrt{1+e^{2t}}dt\approx\frac{f(0)+f(1)}{2}\cdot \frac{1-0}{4}+ \frac{1-0}{4}\cdot\sum_{k=1}^{4-1}{f\Big(0+k\cdot\frac{1-0}{4}\Big)}\\=\frac{\sqrt{2}+\sqrt{1+e^2}}{2}\cdot \frac{1}{4}+ \frac{1}{4}\cdot\sum_{k=1}^{3}{f\Big(k\cdot\frac{1}{4}\Big)}\\=\frac{\sqrt{2}+\sqrt{1+e^2}}{2}\cdot \frac{1}{4}+ \frac{1}{4}\cdot\Bigg(f\Big(\frac{1}{4} \Big)+f\Big(\frac{2}{4} \Big)+f\Big(\frac{3}{4} \Big)\Bigg)\\ \approx 0,53883+0,25\cdot(1,62749+1,92828+2,34130)\approx \underline{\underline{2,01131}} $$
2. WEG
Oder man überlässt es den Computer und lässt ihn wie in der Abbildung unten rechnen:
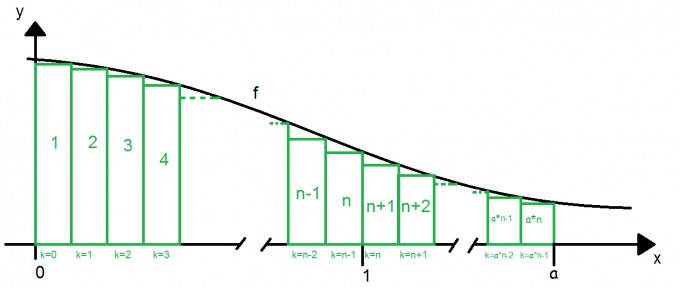
$$ A_k=\frac{1}{n}\cdot f(x),\text{ mit } x:=\frac{k}{n} $$
Dann hat man:
$$ \sum_{k=0}^{a\cdot n-1}{A_k}=\sum_{k=0}^{a\cdot n-1}{\frac{1}{n}\cdot f\Bigg(\frac{k}{n}\Bigg)}=\frac{1}{n}\cdot\sum_{k=0}^{a\cdot n-1}{ f\Bigg(\frac{k}{n}\Bigg)} $$
$$ f(x)=\sqrt{1+e^{2x}} \quad L=\int_{0}^1{\sqrt{1+e^{2x}}dx}\\\stackrel{n=10000}{\approx}\frac{1}{10000}\cdot\sum_{k=0}^{1\cdot10000-1}{\sqrt{1+e^{2\frac{k}{10000}}}}\approx \underline{\underline{2,00342}} $$
Python - Code:
from math import*
n = int(input(' n = ')) #Einteilungsschritte
a = float(input(' a = ')) #Obergrenze
summe = 0
k=0 #Laufvariable k
while k<=a*n-1: #Es wird solange aufaddiert, bis diese Bedingung nicht mehr gilt
summe = summe+sqrt(1+exp(2*k/n) )
k = k+1
print(summe/n)
