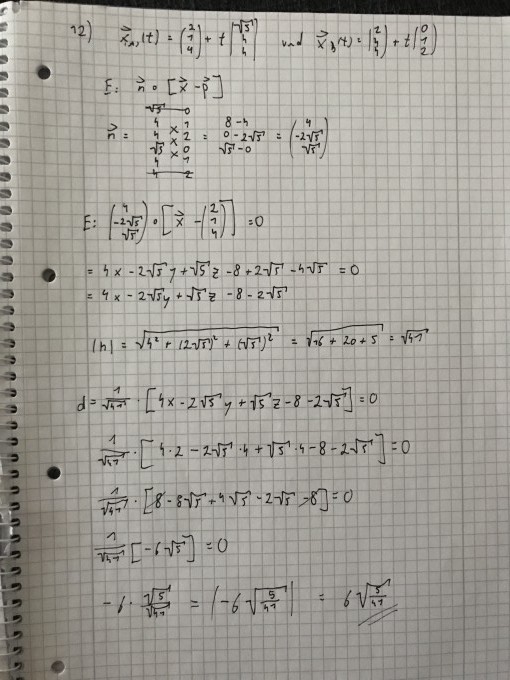Abstandsfunktion für die beiden Schwerpunkte d(t) angeben!

Question

ich habe bei folgender Aufgabe Probleme:

Eine Maschine enthält zwei bewegliche Bauteile, deren Schwerpunkt sich jeweils auf einer Geraden bewegen. Die Positionen xa(t) und xb(t) der Schwerpunkte der Bauteile A und B zum Zeitpunkt t sind gegeben durch:

xa(t) = (2/1/4) + t(wurzel(5)/4/4)

xb(t) = (2/4/4) + t(0/1/2)

Sie suchen zum Zeitpunkt t, zu welchen sich die Schwerpunkte der Bauteile am nächsten kommen!

a) Geben Sie die Abstandsfunktion d(t) der Schwerpunkte der beiden Bauteile zum Zeitpunkt t an:

b) Der minimale Abstand dmin zwischen den Schwerpunkten der Bauteile wird zum Zeitpunkt tmin angenommen. Bestimmen Sie beide Werte!

Den minimalen Abstand hab ich berechnet (Bild)!

Ich weiß nurnicht wie ich a) lösen soll und wie ich die Zeit angeben kann, bzw. wird die Zeit berechnet wenn ich den Abstand mit einer der beiden Funktionen gleich setze und nach t umstelle?

Sorry das es etwas länger geworden ist und danke schonmal für die Hilfe

mfg

Answer 1

Dunkel ist Deiner Rechnung Sinn:

Der Abstand sollte, mit einigen sinnvollen Annahmen, darzustellen sein als

\(d(t) \,:= ((xA(t) - xB(t))^2)\)

also

\(d(t) \, :=  \, 18 \; t^{2} - 18 \; t + 9\)

d'(t)=0 >> t=1/2

\(\sqrt{d(\frac{1}{2})}=\frac{3}{\sqrt{2}}\)

PS:

xa=xA(t):=A+t v_a, xb=xB(t):=B + t v_b

t=0 xA ist in A und xB ist in B, A bewegt sich schneller als B