Flächeninhalt eines Dreiecks

Question

Wir müssen über die Ferien folgende Aufgabe schriftlich bearbeiten, doch ich komme einfach nicht weiter. Ich bin für jeden Hilfe dankbar.

Auf den Seiten BC und CD des Quadrates ABCD liegen die Punkte E bzw. F.

Man beweise: Wenn die Punkte A, E und F die Eckpunkte eines gleichseitigen Dreiecks sind, dann ergibt die Summe der Flächeninhalte der Dreiecke ABE und AFD den Flächeninhalt des Dreiecks ECF.

Answer 1

Zu zeigen ist  ab=(a-b)²/2 oder (1) 2ab=(a-b)²

unter der Bedingung (2)√(a²+b²)=√2(a-b)

(2) quadrieren und (1) einsetzen.

Answer 2

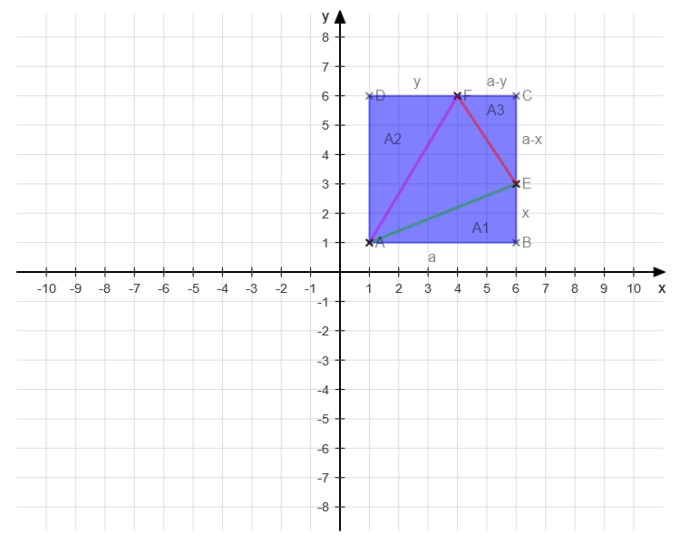
Damit gelten folgende Gleichungen, wenn das Dreieck gleichseitig sein soll.

$$ a^2 +x^2 = a^2 +y^2 $$ also $$ x = y $$

und $$ a^2 + x^2 = (a-x)^2 + (a-y)^2 $$ Mit \( x = y \) folgt $$ x = a(2-\sqrt{3}) $$

Für die Flächen gilt $$  A_1 + A_2 = a^2(2-\sqrt{3}) $$ und $$ A_3 = \frac{ \left[  a- a(2-\sqrt{3}) \right]^2 }{ 2 } = a^2 (2-\sqrt{3}) $$

Also gilt $$ A_1 + A_2 = A_3 $$

Comments

danke für die schnelle Antwort, aber wie kommst du auf dieses

Mit x = y folgt x = a(2 - √3) ?

Das verstehe ich nicht

---

Du hats die Gleichung $$ a^2 + x^2 = (a-x)^2 + (a-y)^2 $$ Hier für \( y \) durch \( x \) ersetzten und die quadratische Gleichung lösen.