Extremstellen berechnen von gebrochenrationaler Funktion: y = (x-2)/(x^2+4)

Question

Aufgabe: Berechnen Sie die Extrempunkte:

y = (x-2)/(x^2+4)

Wie gehe ich hier vor?

Answer 1

Mit der Quotientenregel ableiten und dann gleich null setzen.

Answer 2

y=(x-2)/(x²+4)       Extrempunkte?

Bestimme f '(x) mit der Quotientenregel:    \( [\frac{u}{v}] ' = \frac{u'·v - u ·v'}{v^2} \)

f '(x) = \( \frac{ 1·(x^2+4)-(x-2)·2x} {(x^2+4)^2}=\frac{-x^2+4x+4}{(x^2+4)^2}\)

f '(x) = 0   →  -x² + 4x + 4 = 0  →  x² - 4x - 4 = 0

   pq-Formel  →  x_1,2 = 2 ± 2·√2  (sind die möglichen Extremstellen)

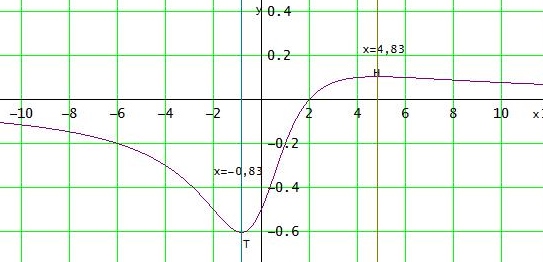
           mit  VZW von f' von + → -   bei   x₁  ≈  4,83    →  Maximalstelle

                  VZW von f' von - → +   bei  x₂  ≈  - 0,83   →  Miniimalstelle

f(2-2√2) = ≈ - 0,60    →   T( - 0,83 | -0,6)  

f(2+2√2) = ≈  0,10    →   H( 4,83 | 0,10)  

Gruß Wolfgang