Hallo Alpay,
Wie gebe ich das in den Taschenrechner ein ... ?
Am besten gar nicht!
Das ist mir bei früheren Fragen von Dir schon aufgefallen - Du stützt Dich zu sehr auf den TR und auf die Rechenwege ab. Du solltest Dich um das Verständnis bemühen, dann hast Du es auch leichter.
Das obige kannst Du im Kopf ausrechnen - das Ergebnis ist \(\alpha =60°\)!
Das geht wie folgt: Im Zähler steht ein Skalarprodukt zweier Vektoren. So schön, wie es Silvia Dir hingeschrieben hat ... kannst Du rechnen:$$\begin{array}{rcrcr} 4 & \cdot & 2 &= & 8 \\ 2& \cdot & -2 &= & -4 \\ 2 & \cdot & 4 &=& 8 \\ \hline &&&& 12\end{array}$$Nur das Ergebnis ist größer als 10 - das sollte ab der 2.Klasse zu machen sein.
Der Nenner besteht aus dem Produkt von zwei Beträgen. Die Beträge sind die Wurzeln der Quadratesummen. Dabei ist es egal, welches Vorzeichen die Koordinaten haben und die Reihenfolge ist auch egal. Nun kommen in beiden Vektoren aber nur die Zahlen \(2, \, 2, \, 4\) vor. Folglich steht da$$\left(\sqrt{2^2 + 2^2 + 4^2}\right)^2 = 2^2 + 2^2 + 4^2 = 24$$Jetzt noch Zähler durch Nenner teilen - auch das sollte ebenso seit der Grundschule zu machen sein - gibt dann:$$\cos \alpha = 12 \div 24 = 0,5$$Nun wird es ein bisschen schwieriger. Was ist der Kosinus? Dazu werfen wir einen Blick auf den Einheitskreis:
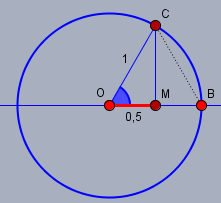
Der Kosinus ist die Projektion des Radius des Einheitsreises auf die Horizontale. Oder eben auch Ankathete (\(|OM|\) rot) zu Hypotenuse (den Radius \(|OC|=1\)). Wenn diese rote Strecke \(|OM|=0,5\) ist, dann liegt der Endpunkt \(M\) genau in der Mitte zwischen \(O\) und \(B\). D.h. das Dreieck \(\triangle OMC\) ist gespiegelt identisch zum Dreieck \(\triangle BMC\). Da \(|OB|\) und \(|OC|\) aber \(=1\) sind und somit auch \(|CB|=|OC|=1\) ist das Dreieck \(\triangle OBC\) ein gleichseitiges mit drei gleichen Winkeln a \(60°\).
Der blaue Winkel ist \(60°\) und der Kosinus von \(60°\) ist \(1/2\). $$\cos 60° = \frac 12$$Mit Sinus und Kosinus ist der Einheitskreis ein Muss. Dann brauchst Du bei mehr als der Hälfte Deiner trigonometrischen Aufgaben keinen TR mehr!
Gruß Werner