1. Voraussetzungen
Der Mathematik wird ein sogenannter Turmcharakter zugeschrieben. Dies soll darauf hinweisen, dass neue Themen meistens auf einem Fundament aufbauen und dass das ganze Gebäude (der Turm) einstürzen kann, wenn das Fundament nicht solide ist. Im Falle der quadratischen Funktionen sind die binomischen Formeln ein wichtiger Teil des Fundamentes:
Erste binomische Formel: (a+b)²=a²+2ab+b²
Zweite binomische Formel: (a–b)²=a²–2ab+b²
Dritte binomische Formel: (a+b)(a–b)=a²–b².
Zur Lösung der Aufgabe x²+4x+3=0 schreibt man im ersten Zugriff eine Seite einer binomischen Formel darunter
x²+ 4x+3=0
a²+2ab+b²=
Ein Vergleich dieser beiden Zeilen führt zu x²=a² oder x=a. Und 4x=2ab führt nach Einsetzen von x für a zu 4x=2xb oder b=2. Dann aber ist b²=4 und nicht 3, wie der direkte Zeilenvergleich nahelegt. Daher Addieren wir in der ersten Zeile auf beiden Seiten eine 1 (die sogenannte „quadratische Ergänzung“) und erhalten:
(*) x²+ 4x+4=1
Die linke Seite dieser Gleichung (*) kann nach der ersten binomischen Formel umgeformt werden und wir erhalten die äquivalente Gleichung
(**) (x+2)²=1
Zieht man in Gleichung (**) auf beiden Seiten die Wurzel, erhält man:
x+2=1 oder x+2= – 1 und dann x=–1 bzw. x=–3. Die gegebene quadratische Gleichung hat zwei verschiedene Lösungen.
An einer Stelle dieses Lösungsweges musste die „quadratische Ergänzung“ gefunden werden. In der Gleichung
(i) x²+px+q=0
ist (p/2)²-q die quadratische Ergänzung. Diese auf beiden Seiten der Gleichung (i) addiert, ergibt
(ii) x²+px+(p/2)²= (p/2)² –q
Und die linke Seite der Gleichung (ii) kann nach der ersten binomischen Formel umgeformt werden. Wir erhalten
(iii) (x+p/2)²= (p/2)² –q.
Zieht man in Gleichung (iii) auf beiden Seiten die Wurzel, erhält man:
(iv) x+p/2= ±√[(p/2)² –q].
Und dann die beiden Lösungen (v) x1/2=–p/2±√[(p/2)² –q].
Die Gleichung (v) heißt „pq-Formel“. Wer sie auswendig kennt, kann mit ihrer Anwendung jede Gleichung der Form (i) lösen.
2. Darstellungsformen quadratischer Funktionen
Die allgemeinste Form einer quadratischen Funktion wird auch „Normalform“ genannt: f(x)=ax²+bx+c. Für a=1 ist damit eine Normalparabel gegeben. Für a>0 ist die Parabel nach oben geöffnet, für a<0 ist die Parabel nach unten geöffnet. |a| ist ein Maß für die Stauchung und Streckung in y-Richtung.
Eine Parabel mit der Gleichung f(x)=a(x–b)²+c hat den Scheitelpunkt (b|c). Daher wird f(x)=a(x–b)²+c auch „Scheitelpunktform“ genannt. Eine Parabel mit der Gleichung in Nullstellenform f(x)=a(x–b)(x–c) a≠0 hat die Nullstellen x1=b und x2=c. An Nullstellen ist f(x)=0 und die quadratische Gleichung 0= a(x–b)(x–c) wird nach dem Satz vom Nullprodukt gelöst: Ein Produkt ist gleich Null, wenn einer der Faktoren Null ist.
Die Darstellungsformen quadratischer Funktionen lassen sich ineinander umformen. Dies wird exemplarisch vorgeführt.
Normalform in Scheitelpunktform:
f(x)=3x²+5x+2
f(x)/3=x²+5/3·x+2/3
f(x)/3–2/3 =x²+5/3·x
f(x)/3–2/3+ (5/6)²=x²+5/3·x+ (5/6)²
f(x)/3–2/3 + 25/36=(x+5/6)²
f(x)/3+ 1/36=(x+5/6)²
f(x)/3=(x+5/6)²– 1/36
f(x) =3·(x+5/6)² – 1/12.
Scheitelpunktform in Normalform:
f(x)=2(x-3)²+5
f(x)=2(x²-6x+9)+5
f(x)=2x²-12x+18+5.
f(x)=2x²-12x+23
Normalform in Nullstellenform:
f(x)=3x²-9x+6
Faktor 3 vor x² ausklammern:
3(x²-3x+2)
Nullstellen von x²-3x+2 bestimmen (pq-Formel):
x1/2=3/2±√(9/4-2)=3/2±√(1/4) x1=1; x2=2
f(x)=3·(x-1)·(x-2).
Die Umformung der Nullstellenform in die Normalform geschieht durch Auflösen der Klammern.
Nullstellenform in Scheitelpunktform:
Die x-Koordinate xs des Scheitelpunktes liegt in der Mitte zwischen den Nullstellen. xs=(x1+x2)/2 die y-Koordinate ys=f(xs). Der Vorfaktor des quadratischen Terms wird übernommen.
Scheitelpunktform in Nullstellenform:
f(x)=2(x-3)²-2
f(x)=2x²-12x+16=2(x²-6x+8)
Nullstellen mit pq-Formel x1=4, x2=2
f(x)=2(x-4)(x-2).
3. Typische Aufgaben zu quadratischen Funktionen
3.1. Optimierungsaufgaben
Aufgabe 1: Welches Rechteck mit dem Umfang 12 hat den größten Flächeninhalt A?
Lösung: 2·(a+b)=12, also a+b=6 und b=6-a.
A=a·b=a·(6–a). Nullstellen bei a_{1}=0 und a_{2}=6
Scheitelpunkt ist höchster Punkt und liegt in der Mitte zwischen 0 und 6. Also ist as=3 und bs=6-as=6–3=3. Das größte Rechteck ist ein Quadrat mit der Seitenlänge a=3.
Aufgabe 2: Ein Sportplatz hat die Form eines Rechtecks (Fußballfeld) mit zwei angesetzten Halbkreisen. Der Umfang des Platzes ist 400 m.
Welche Abmessungen hat ein Fußballfeld größtmöglicher Fläche A?
Lösung: Der Radius der beiden Halbkreise sei r. Der Fußballplatz hat die Länge b und die Breite 2r. Dann gilt 2πr+2b=400 und daher (1) b=200–πr und (2) A=2rπb. (1) in (2) eingesetzt: A=2r·(200–πr). Das ist eine Parabelmit den Nullstellen r=0 und r=200/π. Scheitelpunkt bei r=100/π≈31,83. Abmessungen des Fußballfeldes: Breite 2r≈63,66 m, Länge b=100 m.
3.2. Steckbriefaufgaben
Aufgabe 1: Eine Parabel mit der Scheitelpunkt S(2|-3) geht durch P(0|0).Wie lautet ihre Gleichung in Normalform?
Lösung: P(0|0) einsetzen in die Scheitelform
y=a·(x– 2)² – 3.
0=a·(– 2)² – 3
0=4·a– 3 oder a=3/4.
Also y=3/4·(x-2)² – 3 auflösen y=3/4·(x²+4x+4)-3 oder y=3/4·x²– 3x+3– 3 und dann y=3/4·x²– 3x.
Aufgabe 2: Welchen Scheitelpunkt hat eine Parabel durch P(0|8), Q(1|3) und R(2|0)?
Lösung: P,Q und R in den Ansatz y = ax²+bx+c einsetzen:
(1) 8=c
(2) 3=a+b+c
(3) 0=4a+2x+ c
C=8 in (2) und (3) einsetzen:
(i) 3=a+b+8
(ii) 0=4a+2b+8
Gleichung (i) umformen (iii) -20=4a+4b
Gleichung (ii) umformen (iv) –8=4a+2b
Subtrahieren –12=2b oder b=–6 in (ii) einsetzen:
0=4a–12+8 oder a=1.
Die Normalform y=x²–6x+8 in die Scheitelpunktform umwandeln:
y+1=x²–6x+9
y+1=(x–3)²
y=(x–3)² –1
Scheitelpunkt (3|–1).
3.3 Schnittpunktaufgaben
Aufgabe 1: Welche Schnittpunkte haben die Parabeln mit den Gleichungen y=2x²+5x+10 und y=3x²+x+13?
Lösung: Parabelgleichungen subtrahieren: 0=x²–4x+3. x1/2=2±√(4-3). x1=3; x2=1. Einsetzen in ein der beiden Parabelgleichungen: y1=43; y2=17. Schnittpunkte: (3|43) und (1|17).
Aufgabe 2:
a) In welchen Punkten schneidet die Gerade mit der Gleichung y=4x-3 die Parabel mit der Gleichung y=x²?
b) Löse Aufgabe a) graphisch.
Lösung: a) Gleichungen subtrahieren: 0=x²-4x+3. x1/2=2±√(4-3). x1=3; x2=1. Einsetzen in die Parabelgleichung: y1=9 und y2=1. Schnittpunkte: (3|9) und (1|1).
b) → → → →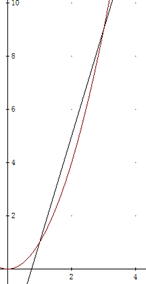
So löst man auch die quadratische Gleichung 0=x²–4x+3 mit graphischen Mitteln.