Steckbriefaufgaben Bedingungen: Graph berührt x-Achse im Ursprung

Question

Aufgabe:

Bestimmen Sie die Gleichung einer ganzrationalen Funktion 3.Grades, deren Graph die x-Achse im Ursprung berührt und deren Tangente in P(-3/0) parallel zu y=6x ist.

Ich habe nur  3 Bedingungen herausgefiltert,undzwar

1. f (0) =0

2. f (-3) =0

3. f ' (-3) =6

Aber mir fehlt die 4 Bedingung und ich komme einfach nicht darauf.

Answer 1

Graph die x-Achse im Ursprung berührt

f(0)=0

f'(0)=0, da der Graph sie sonst nicht nur berühren würde.

Comments

Heeee? Warum denn jetzt f ' (0)=0 ? Woher weisst man das?

---

Der Graph geht doch durch (0/0) und wenn die 4 Bedingung f'(0)=0 ist,dann wäre es doch ein Hoch/Tiefpunkt

---

Es steht doch im Text "BERÜHRT" und nicht schneidet. Und das geht eben nur, wenn an dieser Stelle ein Extremum liegt, bzw. eine Änderung der Steigung (pos. / neg.) vorliegt, da der Graph die Abszisse sonst kreuzen würde.

Answer 2

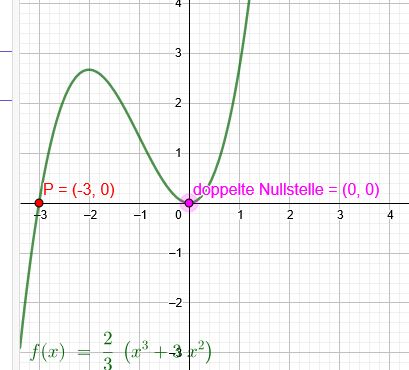
Bestimmen Sie die Gleichung einer ganzrationalen Funktion 3.Grades, deren Graph die x-Achse im Ursprung berührt und deren Tangente in P\((-3|0)\) parallel zu y=6x ist.

Graph berührt x-Achse im Ursprung →doppelte Nullstelle.

P\((-3|0)\) →einfache Nullstelle

\(f(x)=ax^2(x+3)=a(x^3+3x^2)\)

Tangente in P\((\blue{-3}|0)\) parallel zu \(y=\red{6}x\)

\(f'(x)=a(3x^2+6x)\)

\(f'(\blue{-3})=a(27-18)=9a=\red{6}\)

\(a=\frac{6}{9}=\frac{2}{3}\):

\(f(x)=\frac{2}{3}(x^3+3x^2)\)