Stereometrie: Kegel und 2 Kugeln

Question

Aufgabe:

Einem Kegel sind 2 Kugeln (r1 4cm und r2 9 cm) eingeschrieben, die sich gegenseitig und den Kegelmantel berühren. Die grössere berührt zusätzlich die Grundfläche des Kegels.

a) Berechnen Sie den Grundkreisradius und die Höhe des Kegels.

b) Welche Radien haben die Berührungskreise der beiden Kugeln mit dem Kegelmantel?

Problem/Ansatz:

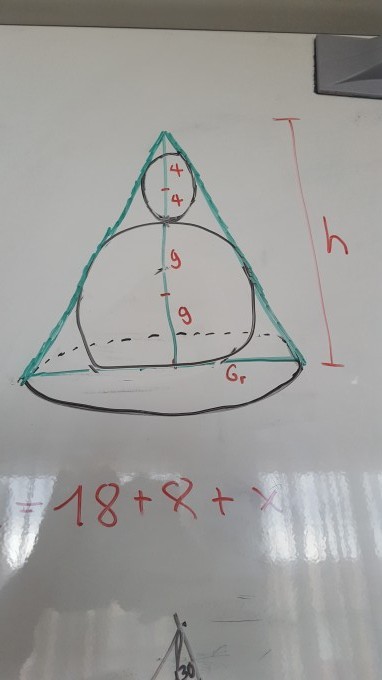
Ich habe es so oft versucht, aber ich sehe einfach nicht den geometrischen Zusammenhang, mit dem ich das berechnen kann. Meine Skizze:

Answer 1

Nun, ich weiss nicht mit welchem Handwerkszeug (eventuell Strahlensatz) Du arbeiten willst, deshalb erstmal einen Plan

und ein paar Zwischenergebnisse

S:=(0, 162 / 5)

G:=(27 / 2, 0)

Würde das für einen Einstieg ausreichen?

Comments

Mein Strahlensatz sieht so aus: 13 + k / 22 + k = 9 / r3 Aber ich habe ja zwei Unbekannte, wie soll das funktionieren?

---

Zum Stahlensatz sehe ich

r1/r2=k/(k+r1+r2)

---

Jetzt habe ich das gesehen. Mich hat eben das r3 verwirrt, weil du das rot gemacht hast, dachte ich, dass das damit verbunden ist.

---

r3 (G) - Kegelradius wäre noch zu berechnen..

Nun haben wir die Höhe (S)? Hast Du den Weg gefunden?

---

Ich habe alles gelöst von a. Gr = 13.5 cm

H = 32.4 cm

Wie muss ich die Aufgabe b verstehen? Was meinen die mit Berührungsradien?
Was ist ein Berührungskreis? Ich verstehe das irgendwie nicht.

---

Alles gut - prima gemacht!

Eine Kugel berührt den Kegel in einem "Schnittkreis" dessen Radius Du von T1 oder T2 senkrecht zur Achse des Kegels sehen kannst - also von T1/T2 parallel zu r3 messen.

Kannst Du die Winkelfunktionen sin/cos einsetzen?

---

Ja, die kenne ich, aber ich verstehe die Geometrie immer noch nicht. Also eine Kugel berührt den Kegelmantel und dann entsteht dort ein Kreis. Das kann ich mir noch vorstellen. Wie meinst du das mit Achse und senkrecht und parallel, kannst du mir das vielleicht aufzeigen in deinem Bild?

---

T1/T2 parallel zu r3 messen. Wenn ich das lese, dann verstehe ich nichts darunter.

---

Ok, r5 wäre der Radius des Berührkreises der kleinen Kugel:

---

Die Frage wäre jetzt, wie sieht es mit den Winkeln in diesem kleinen Dreieck aus. Ich kann nicht sagen, wie die lauten. Ich brauche die für die Trigonometrie. Ich weiss, dass die eine Seite senkrecht auf der Höhe ist, dass heisst, das es einen 90 Grad winkel hat, aber was ist mit den anderen zwei ?

---

Ist das ein halbes gleichseitiges Dreieck? 30 60 90?????

---

Aus dem Dreieck mit r1 und k ⊥ bei T1 erhältst Du

cos(α)=r1/k  

===> α = 67.38°

und damit dann r5

 

---

Dankeeeeeee! Ich bin zu dumm, um sowas zu sehen. Du bist ein Genie. Vielen Dank für deine Hilfe!

---

Ajee, da nicht für... ;-)

Einen Punkt für die selbstständige Arbeitsweise nach den Anschiebern - ist nicht selbstverständlich hier!

---

Und das mit der selbständigen Arbeitsweise sollte auf jeden Fall selbstverständlich sein, denn wir sind hier um etwas zu lernen und nicht, um unsere Hausaufgaben von jemandem machen zu lassen. Ich versuche immer alles und wenn ich gar nicht mehr weiterkomme, dann frage ich nach.