Gegeben sit die Funktion fk : x → x4 – x2 mit x ∈ ℝ und k > 0
"Untersuchen Sie die Funktionsschar fk allgemein nach dem zuvor angegebenen Schema und skizzieren Sie die Funktion der Schar für k =1 und k = 2 gemeinsam in einem Koordinatensystem"
Könnte jemand für mich sicher machen das ich alles richtig habe??
Also, nach dem Schema:
I. Bestimmung der Definitionsmenge. (Die Wertemenge sollte zu Beginn nur bestimmt werden, falls sie einfach zu erkennen und für die weitere Untersuchung nützlich ist.)
D = ℝ
II. Globales Verhalten der Funktion für sehr kleine und sehr große x-Werte.
x → + ∞ : f(x) → + ∞
x → – ∞ : f(x) → + ∞
III. Bestimmung der Symmetrie, ob die Funktion achselsymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung ist (oder ob andere aussagen zur Symmetrie gemacht werden können.)
f(x) = x^4 – kx^2
f(–x) = x^4 – kx^2
–f(x) = x^4 + kx^2
f(x) = f(–x) : Achselsymmetrisch zur y-Achse
IV. Bestimmung der Nullstellen und der Art der Nullstellen (ob mit / ohne NZW)
f(x) = 0
f(x) = x^4 – kx^2 = 0 ⇔ f(x) = x^2 (x^2 – k) = 0 ⇒ x1 = 0 ; x2 = +\( \sqrt{k} \) ; x3 = –\( \sqrt{k} \)
Nullstellen: N1( 0 | 0 ) ; N2( \( \sqrt{k} \) | 0 ) ; N3( –\( \sqrt{k} \) | 0 )
VZW Bei N2 und N3.
V. Bestimmung des Schnittpunktes mit der y-Achse.
x = 0 ⇒ f(0) = 0 .. SP(0 | 0)
VI. Bestimmung der 1., 2. und 3. Ableitung.
f(x) = x^4 – kx^2 ; f'(x) = 4x^3 – 2kx ; f''(x) = 12x^2 – 2k ; f'''(x) = 24x
VII. Bestimmung der Extrempunkte.

VIII. Bestimmung der Wendepunkte und gegebenenfalls Sattelpunkte.

IX. Erstellung einer Wertetabelle für den interessanten Bereich der Funktion, in der Nähe der zuvor gefundenen Nullstellen sowie der Hoch-, Tief- und Wendepunkte.
Das Krieg ich schon hin :)
X. Bestimmung der Wartemenge, falls nicht schon zu beginn erfolgt.
W = R??
XI. Zeichnen des Graphen der Funktion
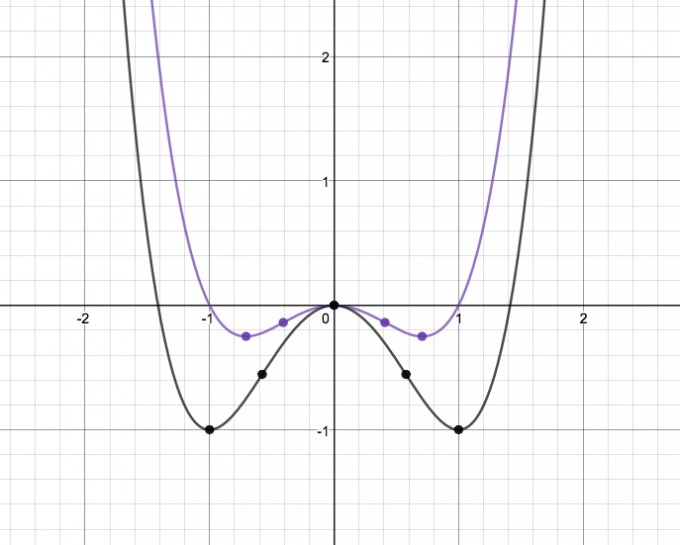
Vielen Dank im Voraus!