Die Tangens-Funktion tan x= sin x /cos x ist stetig und streng monoton wachsend in
Die Umkehrfunktion in diesem Intervall ist der Arcustangens arctan.
a) Was ist der maximale Definitionsbereich D max (arctan) und der Wertebereich W(arctan) ?
D = R
W = ]-pi/2 ; pi/2[
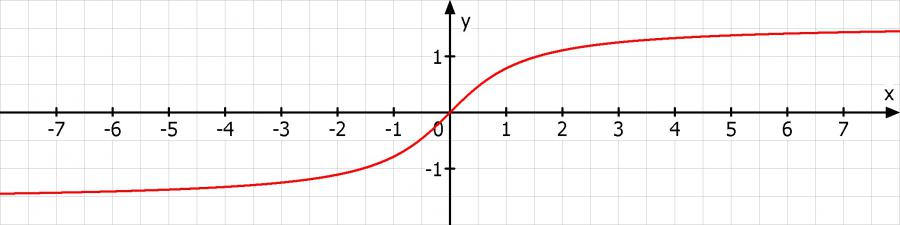
(b) Zeichnen Sie die Graphen von tan und arctan in ihren jeweiligen maximalen Defini-
tionsbereichen.
Hier die Tangensfunktion:

und die Arcustangens Funktion