Gegeben ist die Funktion f durch die Gleichung f(x)=0,5x2*e^(-x+2)

Question

Aufgabe:

1.)Bestimmen Sie die erste und zweite Ableitung

2.)Weisen Sie nach, dass ein lokaler Hochpunkt existiert und geben Sie die Koordinaten des Hochpunktes an.

Problem/Ansatz:

Ich würde gerne die Rechenschritte haben, dass ich die Rechnung nachvollziehen kann.

Answer 1

Benutze zur Hilfe auch: https://www.ableitungsrechner.net

[0.5·x²·e^(-x + 2)]'

Produktregel

= [0.5·x²]'·e^(-x + 2) + 0.5·x²·[e^(-x + 2)]'

= x·e^(-x + 2) + 0.5·x²·(-e^(-x + 2))

= x·e^(-x + 2) - 0.5·x²·e^(-x + 2)

e-Funktion ausklammern

= (x - 0.5·x²)·e^(-x + 2)

Comments

[(x - 0.5·x²)·e^(-x + 2)]'

= [(x - 0.5·x²)]'·e^(-x + 2) + (x - 0.5·x²)·[e^(-x + 2)]'

= (1 - x)·e^(-x + 2) + (x - 0.5·x²)·(-e^(-x + 2))

= (1 - x)·e^(-x + 2) - (x - 0.5·x²)·e^(-x + 2)

= ((1 - x) - (x - 0.5·x²))·e^(-x + 2)

= (1 - x - x + 0.5·x²)·e^(-x + 2)

= (1 - 2·x + 0.5·x²)·e^(-x + 2)

Answer 2

f ( x ) = 0.5 * x² * e^( -x + 2 )
Produktregel
( u * v ) ´ = u´ * v + u * v´

u = 0.5 * x²
u ´= x
v = e^( -x+ 2)
v ´= e^( -x+ 2) * (-1 ) = - e^( -x+ 2)

( u * v ) ´ = x * e^( -x + 2)   +  0.5 * x² * - e^( -x+ 2)

x * e^( -x + 2)  -  0.5 * x² *  e^( -x+ 2)
e^( -x + 2) * ( x  -  0.5 * x² )

Comments

Hier die 2.Ableitung

---

f ´( x ) = e^( -x + 2) * ( x  -  0.5 * x2 )
Stelle mit waagerechter Tangente
e^( -x + 2) * ( x  -  0.5 * x2 ) = 0
Satz vom Nullprodukt anwenden
Die e Funktion ist stets ungleich null, also
x  -  0.5 * x² = 0
x * ( 1 - 0.5 * x ) = 0
Satz vom Nullprodukt
x = 0
und
1 -0.5 * x = 0
x = 2

Muß jetzt erst zum Mittagessen

Versuch einmal herauszufinden ob x = 0
bzw. x = 2 ein Hochpunkt ist.

Answer 3

y=0.5x²*e^(-x+2)

------>Produktregel

u= 0.5 x² ,  v=e^(-x+2)

u' = x         ,  v'= -e^(-x+2)

y' =u' v+ u v'

y'= x *e^(-x+2) +0.5 x² * (-)e^(-x+2)

y'=e^(-x+2) (x - x²/2)

analog die 2.Ableitung

Extremwerte:

y'=0

e^(-x+2) (x - x²/2)=0

Satz vom Nullprodukt:

e^(-x+2) ----<keine Lösung

x(1-x/2)=0

x₁=0

x₂=2

Nachweis Art des Extremums :2. Ableitung:

Comments

y '' =e^(-x-2)/2 (x ² -4x+2)

y''(2)= -1<0 ------->Maximum

y''(0)= e² >0 ------>Minimum

Geben Sie die Koordinaten des Hochpunktes an.

y=0.5x²*e^(-x+2)

y(2)= 0.5 *2² e⁰

y(2)= 2

----------->

H (2/2)

Answer 4

Erste Abletung nach Produkt und Kettenregel bilden. Kontrollergebnis $f'(x) = \frac{ e^{2-x} \ x \ (2 - x) } { 2 }$

Zweite Ableitung ebenfalls nach Produkt und Kettenregel bilden. Kontrollergebniss $f''(x) = \frac{ e^{2 - x} \ (x^2 - 4x +2) } {2}$

Damit gibt es zwei kritische Punkte die aus der Gleichung $f'(x) = 0$ folgen, nämlich $x_0 = 0$ und $x_1 = 2$

Damit gilt $f''(0) = e^2 > 0$, also liegt bei $x_0$ ein Minimum vor, nämlich $f(0) = 0$ und $f''(2) = -1 < 0$, also liegt bei $x_1$ ein Maximum vor, nämlich $f(2) = 2$

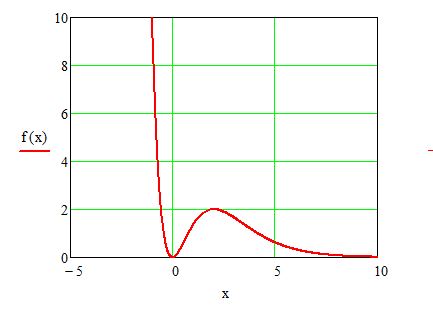
Die Kurve sieht dann so aus