Hypothesentest: Summe der Fehlerwahrscheinlichkeiten minimieren

Question

Aufgabe:

$$\begin{array}{l}{\text { Die Zauberkünstlerin Aida besitzt einen magischen Zylinder, aus dem sie mit Wahrschein- }} \\ {\text { lichkeit } p \text { weilße und ansonsten schwarze Kaninchen hervorzaubert. Der Ausgang des Zau- }} \\ {\text { bertricks ist hierbei unabhängig von vorherigen Versuchen. Leider ist Aida der exakte }} \\ {\text { Wert von } p \text { unbekannt. Der Hersteller des Hutes versichert inr jedoch, dass entweder }} \\ {H_{0} : p=1 / 4 \text { oder } H_{1} : p=3 / 4 \text { gilt. Um die beiden Hypothesen zu testen, zaubert Aida }} \\ {n \text { Kaninchen herbei und betrachtet die Zahl } X \text { der weißen Exemplare. }}\end{array}$$

$$\begin{array}{l}{\text { Sei } K \subseteq\{0, \ldots, n\} \text { Aidas Ablehnungsbereich für } H_{0} \text { bezüglich der Testgrösse } X . \text { Wie }} \\ {\text { muss Aida } K \text { in Abhängigkeit von } n \text { wählen, sodass die Summe des Fehlers erster }} \\ {\text { und des Fehlers zweiter Art minimal ist? }}\end{array}$$

Problem/Ansatz:

Mein Ansatz bisher:

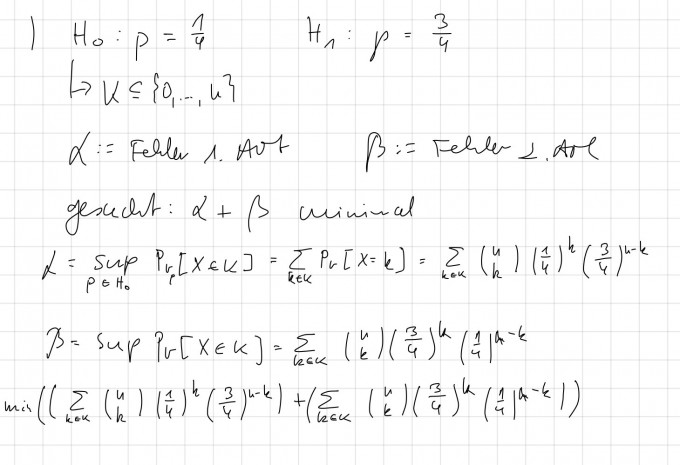
leider weiß ich jetzt nicht wie ich hierraus das Minimum, in Abhängigkeit von K bilden soll, kann mir jemand weiterhelfen?

Vielen Dank im Voraus!

Comments

Der \(\beta\)-Fehler ist ja, wenn \(H_0\) beibehalten wird, obwohl \(H_1\) richtig ist. Der Index der entsprechenden Summe stimmt also nicht.

---

Für \(K=\{k,...,n\},\quad 0\le k\le n\)   konnte ich die Summe der Fehler zu

$$\sum_{i=0}^{n-k}{\binom{n}{i}\cdot\left(\frac{1}{4}\right)^{n-i}\cdot\left(\frac{3}{4}\right)^{i}}\quad+\quad\sum_{i=0}^{k-1}{\binom{n}{i}\cdot\left(\frac{1}{4}\right)^{n-i}\cdot\left(\frac{3}{4}\right)^{i}}$$

vereinfachen (wenn ich keine Fehler gemacht habe).

Mit der Eigenschafte \(\binom{n}{k}=\binom{n}{n-k}\) könnte man hier wahrscheinlich in einem kurzen Aufsatz erklären, dass die Summe der Fehler für \(k=\lceil\frac{n}{2}\rceil\) (und wenn n gerade ist, auch für \(k=\frac{n}{2}+1\)) minimal ist.

---

Vielen Dank! Müsste richtig sein!

Answer 1

Um die Summe aus α- und β-Fehler zu minimieren muss man sich bei einem Ausgang immer für die Hypothese entscheiden, die für diesen Ausgang die größte Wahrscheinlichkeit liefert.

Zaubert Aida also mehr weiße als schwarze Kaninchen hervor sollte sie sich für H1 entscheiden. Zaubert sie mehr schwarze als weiße hervor, dann sollte sie sich für H0 entscheiden.

Sind es gleich viele weiße wie schwarze, sollte sie den Test wiederholen.

Comments

Andersrum wird ein Schuh draus :)

Und eine Wdh. ist, wenn auch sinnvoll, von der Frage nicht wirklich vorgesehen.

---

Richtig. Ich hatte H0 und H1 vertauscht.

Wenn keine Wdh. vorgesehen ist, dann ist es egal wie man sich entscheidet.

Übrigens lässt sich das minimum recht deutlich für ein bestimmtes Beispiel am Diagramm der Wahrscheinlichkeitsverteilung zeigen.