Hallo ich komme gerade bei einer Aufgabe nicht weiter und würde mich freuen, wenn mir jemand einen Tipp geben könnte:
Als JOHANNES KEPPLER (1571 - 1630), kaiserlicher Hofmathematicus zu Linz an der Donau, sich um zweiten Mal verheiratete, erregte beim Kauf eines Fasses Wein die folgende Methode des Weinhändlers zur Ermittlung des Preises seinen Unwillen:
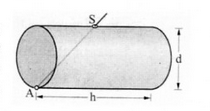
Dieser verwendete eine Messrute, steckste sie in das Spundloch S (welches in der Mitte des Fasses liegt) hinein, so dass ihr Ende bei A an den Boden des Fasses reichte, maß die Länge \(l=\overline{AS}\) (in der Fachsprache Visierlänge) und legte dann den Preis fest.
KEPLER war sich bewusst, dass es zu einer festen Visierlänge l sehr viele Weinfässer mit unterschiedlichen Volumina gibt und stellte sich die Frage, ob diese Methode vielleicht bei den österreichischen Fässern, welche niedriger und dicker waren als die in seiner schwäbischen Heimat, dennoch zulässig sein könnte.
Ersetzen Sie zur Vereinfachung die in Wirklichkeit bauchigen Weinfässer durch zylinderförmige Fässer.
a) Berechnen Sie h und d bei einer Visierlänge von l = 1,00 m, so dass das Fassvolumen maximal ist.
b) Bestimmen Sie rechnerisch das Verhältnis h:d (h zu d), für das das Fassvolumen maximal ist.
Die Hauptbedingung sollte ja das Zylindervolumen sein (pi*r²*h).
Nur wie sind die Nebenbedingungen?? Wie ich das sehe, habe ich ja weder einen Radius, noch einen Durchmesser - nur eine "Visierlänge". ??