Hallo fawick,
ich kann mit der gegebenen nebenbedingung irgendwie nichts anfangen.
Die Nebenbedingung schränkt die Funktion \(f(x,y)\) ein. Stelle Dir die Funktion \(f(x,y)\) wie eine Gebirge vor und die Nebenbedingung beschreibt einen Pfad durch das Gebirge. Gesucht ist nun die höchste oder tiefste Stelle auf diesem Pfad.
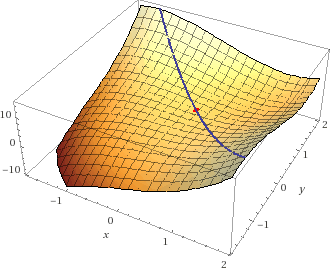
Oben siehst Du das 'Gebirge' und die Gerade \(x+y=5/8\) ist der Pfad, der augenscheinlich bei dem roten Punkt seine tiefste Stelle hat. Diese Stelle ist gesucht.
Mit einem scharfen Blick auf \(f\) und mit dem Plot oben, lässt sich die Aufgabe (fast) ohne Rechnung lösen. Die Funktion \(f\) ist symmetrisch zur Achse \(y=x\) - d.h. Du kannst \(x\) und \(y\) vertauschen und der Funktionswert bleibt erhalten \(f(x,y) = f(y,x)\). Auf dem Plot oben sieht man, dass die Gerade \(x+y= 5/8\) die Symmetrieachse im rechten Winkel schneidet. Folglich liegt auch das Extremum bei \(y=x\). Einsetzen in die Nebenbedingung gibt sofort \(x=y= \frac 45\).
Nachrechnen kann man das u.a. mit dem Lagrange-Verfahren. Dazu stelle man aus der Funktion \(f\) und der Nebenbedingung \(n(x,y)= x+y-5/8=0\) die Lagrange-Funktion auf, und leite diese ab.$$\begin{aligned} L(x,y,\lambda) &= f(x,y) + \lambda \cdot n(x,y) \\ L(x, y, \lambda) &= x^{3} + y^{3} - 3xy + 2 + \lambda\left( x+y - \frac 85\right) \\ \frac{\partial L}{\partial x} &= 3x^2 - 3y + \lambda = 0 \\ \frac{\partial L}{\partial y} &= 3y^2 - 3x + \lambda = 0 \end{aligned}$$aus der ersten Ableitung lässt sich \(\lambda\) isolieren und Einsetzen in die zweite gibt$$\begin{aligned}\implies \lambda &= -3x^2 + 3y \\ 3y^2 - 3x -3x^2 + 3y &= 0 \\ y^2 - x - x^2 + y &= 0\end{aligned}$$In die letzte Gleichung könnte man nun die Nebenbedingung einsetzen und dann \(x\) und \(y\) berechnen. Man kann sie aber auch faktorisieren .. $$\begin{aligned} y^2 - x - x^2 + y &= 0 \\ (y^2 - x^2) + (y - x)&= 0 \\ (y - x)(y+x) + (y - x)&= 0 \\ (y - x)(y+x+1)&= 0\end{aligned}$$Dies ist also erfüllt, wenn \(x=y\) (siehe Lösung oben) oder wenn \(x+y= - 1\) ist. Letzteres steht aber im Widerspruch zur Nebenbedingung, womit die erste Lösung auch die einzige bleibt.