Zeigen Sie: M ist eine 2-dimensionale Untermannigfaltigkeit des ℝ3, Angabe eines Tangentialraums, Skizzee von M

Question

Aufgabe:

Betrachten Sie
M = {x ∈ ℝ³ |x₁² + x₂² − x₃² = 1}
a) Zeigen Sie: M ist eine 2-dimensionale Untermannigfaltigkeit des ℝ³.

b) Skizzieren Sie M .

c) Geben Sie eine Basis des Tangentialraums an a = (1, 1, 1) an.

Answer 1

a)

Sei \(f: \mathbb{R}^3 \to \mathbb{R}, x \mapsto x_1^2+x_2^2-x_3^2-1\), dann gilt:  $$M=\{x\in \mathbb{R}^3 : x_1^2+x_2^2-x_3^2=1\}=\{x\in \mathbb{R}^3 : f(x)=0\}=f^{-1}(\{0\})$$Der Gradient von \(f\) ist $$\nabla f(x_1,x_2,x_3)=(2x_1,2x_2,-2x_3)=0 \Leftrightarrow (x_1,x_2,x_3)=(0,0,0)$$Da aber \((0,0,0)\notin M\), haben wir nach dem Satz vom regulären Wert eine \(3-1=2\)-dimensionale Untermannigfaltigkeit des \(\mathbb{R}^3\).

b)

Das ist ein einschaliges Hyperboloid

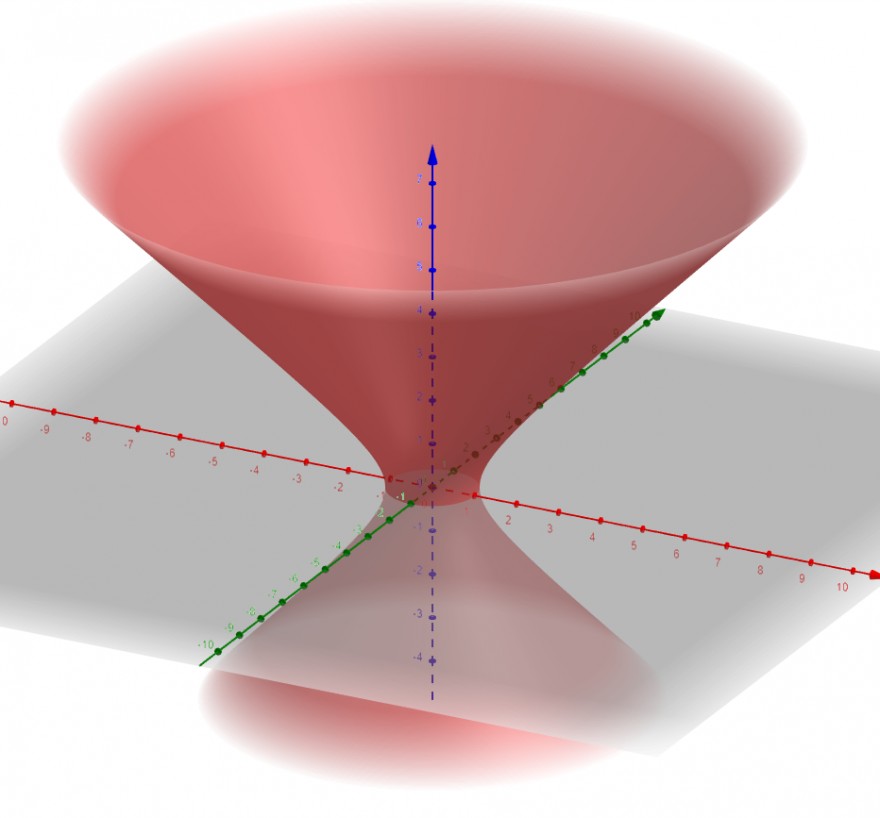
c)

Den Tangentialraum findest du, indem du \(T_{a}M=\text{kern }Df(a)\) berechnest. Eine Basis davon zu finden, kriegst du bestimmt hin!