Aufgabe:
In dieser Aufgabe geht es um die L-periodische Fortsetzung der Funktion \( f(x)=h \cdot \cosh \left(\frac{2 \alpha}{L}\left(x-\frac{L}{2}\right)\right) \) für \( x \in[0, L] \)
a) Skizzieren Sie diese Funktion für ein paar Perioden.
b) Bestimmen Sie die Fourier-Koeffizienten \( c_{n} \) dieser Funktion. Zur Kontrolle, dass Resultat ist \( \frac{h \alpha \sinh (\alpha)}{(n \pi)^{2}+\alpha^{2}} \)
c) Bestimmen Sie die reellen Koeffizienten \( a_{n}, b_{n} \) und \( f_{0} \)
d) Welche Werte sollten die Koeffizienten für \( \alpha=0 \) annehmen. Passt das zu lhrem Resultat aus Aufgabenteil c)?
e) Nutzen Sie nun Ihre \( c_{n} \) aus Aufgabenteil b). Wie müssen die Parameter \( L, h \) und \( \alpha \) gewählt werden, damit Sie die Fourier-Reihe von \( g(x)=\cosh (x) \) für \( x \in[-1,1] \) (und ansonsten 2 -periodisch fortgesetzt) erhalten? Sie müssen zusătzlich eine in der Vorlesung angegebene Eigenschaft der Fourier-Reihe verwenden. Sie sollen die Fourier-Reihe von \( g(x) \) natürlich auch angeben.
Ich habe gestern schon eine ähnliche Aufgabe gelöst und weiß welche Formeln ich anwenden muss, allerdings bekomme ich es einfach nicht hin.
Meine Skizze sieht nicht wie ein Sägezahn sondern wie ein "Sägezahn mit Wellendurchlauf" aus.
Bei Aufgabenteil b) komme ich mit Biegen und Brechen nicht auf das angegebene Resultat.
Ich verwende folgende Formel:
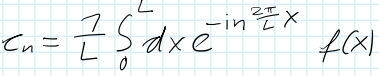
Text erkannt:
\( c_{n}=\frac{1}{L} \int \limits_{0}^{L} d x e^{-i n^{2 \frac{\pi}{L} x}} f(x) \)
Für Tipps und Hilfestellungen wäre ich sehr dankbar!