Aufgabe:
Problem/Ansatz:
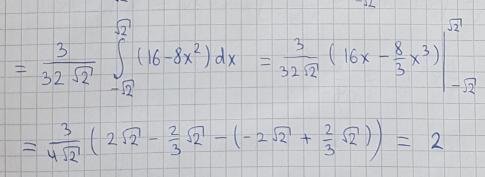
Text erkannt:
\( =\frac{3}{32 \sqrt{2}} \int \limits_{-\sqrt{2}}^{\sqrt{2}}\left(16-8 x^{2}\right) d x=\frac{3}{32 \sqrt{2}}\left(16 x-\frac{8}{3} x^{3}\right)^{\sqrt{2}} \)
\( =\frac{3}{4 \sqrt{2}}\left(2 \sqrt{2}-\frac{2}{3} \sqrt{2}-\left(-2 \sqrt{2}+\frac{2}{3} \sqrt{2}\right)\right)=2 \)
Ich wäre froh, wenn mir jemand erklären würde, wie das aufgelöst wurde !