Bestimmen Sie die orthogonale Projektion p : R3 → R3 auf Bild(A).

Question

Gegeben ist die Matrix A = $\begin{pmatrix} 1 & 1 & 1 \\ -1 & 1 & 0 \\ 0 & 2 &1 \end{pmatrix}$ .

(a) Bestimmen Sie die orthogonale Projektion p : R³ → R³ auf Bild(A).
(b) Berechnen Sie eine Orthonormalbasis von (ker(A))^⊥.
(c) Bestimmen Sie die Pseudoinverse A+ von A.

Answer 1

Hallo,

Sind die Spaltenvektoren von $A$ $u$, $v$ und $w$, so sit hier: $w = (u+v)/2$. Die Spaltenvektoren sind also linear von einander abhängig. Das Bild von $A$ ist folglich eine Ebene, die von zwei der drei Spaltenvektoren aufgespannt wird. So ist das Bild $B$:$$B= \left\{x \in \mathbb R^3: \space n x = 0, \space n= k(u \times v), \space k \in \mathbb R \implies \begin{pmatrix}-1\\ -1\\ 1\end{pmatrix} x = 0 \right\}$$Und der Kern $K$ von $A$ ist die Menge aller $x \in \mathbb R^3$, für die gilt:$$K = \left\{ x \in \mathbb R^3: A \cdot x = 0 \implies x = \begin{pmatrix}1\\ 1\\ -2\end{pmatrix} t, \space t \in \mathbb R\right\}$$Hier sind das Bild (die grüne Ebene) und der Kern (die blaue Gerade) im Bild dargestellt:

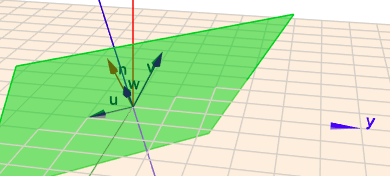
(klick auf das Bild)

Die Projektionsmatrix $P$ auf eine Ursprungsebene mit Normalenvektor $n$ (s.o. und rot im Bild) ist:$$P = \underline 1 - \frac{n \cdot n^T}{\left< n, n\right>} = \frac 13 \begin{pmatrix}2& -1& 1\\ -1& 2& 1\\ 1& 1& 2\end{pmatrix}$$Somit gilt für jedes $x \in \mathbb R^3$$$x' = P \cdot x, \space x' \in B \space \land \space x-x' = k n, \space k \in \mathbb R$$

(b) da der Kern ein 1-dimensionaler Vektorraum ist, besteht seine Orthonormalbasis $B_K$ nur aus einem Vektor der Länge 1$$B_K = \left\{ \frac 1{\sqrt 6 } \begin{pmatrix}1\\ 1\\ -2\end{pmatrix}\right\}$$(s.o.)

(c) die Pseudoinverse $A^+$ - genauer die Moore-Penrose-Inverse - berechnet sich nach dem Verfahren, was hier beschrieben ist. Die Matrizen $B$ und $C$ beziehen sich auf das dort beschrieben Verfahren, nach dem $A = B \cdot C$ gilt. Ich habe:$$\begin{aligned} B &= \begin{pmatrix}1& 1\\ -1& 1\\ 0& 2\end{pmatrix}, \quad C = \begin{pmatrix}1& 0& 0,5\\ 0& 1& 0,5\end{pmatrix}\\ A^+ &= C^T \cdot (CC^T)^{-1} \cdot (B^TB)^{-1} \cdot B^T\\ &= \frac 1{18} \begin{pmatrix}7& -8& -1\\ 1& 4& 5\\ 4& -2& 2\end{pmatrix} \end{aligned}$$Falls Du Fragen dazu hast, so melde Dich bitte.

Comments

Ich versuche gerade GeoGebra der Thematik näher zu bringen und hab bei der Suche deine Antwort gefunden.

Hast du die BC-Zerlegung auch einfach als LGS angesetzt oder hast du was cleveres im Portfolio?

---

Hast du die BC-Zerlegung auch einfach als LGS angesetzt oder hast du was cleveres im Portfolio?

Oh je! Ich kann mich überhaupt nicht dran erinnern, wie ich das damals gemacht habe. Auch der Verweis auf den Wiki-Artikel hinter dem Link (s.o.) bringt mich da nicht weiter, da dort eben genau nicht(!) beschrieben steht, wie man auf $B$ und $C$ kommt.

Ich glaube, dass ich für $B$ einfach die ersten beiden Spalten von $A$ hergenommen habe. Dann ist der linke quadratische $2\times 2$-Teil von $C$ die Einheitsmatrix. Und für die dritte Spalte von $C$ muss es anschließend eine Lösung geben, da der dritte Spaltenvektor von $A$ eine Linearkombination der anderen beiden darstellt. Das ist alles.

$A^+$wird dann nach obiger Formel berechnet.

So weit ich es verstanden habe muss man nur irgendeine gültige Kombination von $B$ und $C$ finden um $A^+$ zu berechnen.

---

Wenn die vorgegebene Matrix wie hier keinen vollen Rang hat, um die Pseudoinverse direkt zu berechnen, wird bei uns an der Uni meistens mit der Vollrang-Faktorisierung oder einfach direkt mit der Singulärwertzerlegung gearbeitet. Tricks um das teils viele Rechnen zu umgehen gibt es wohl nur in konstruierten Spezialfällen

---

@Werner

Ja, das war auch meine Idee r lin.unabhängige Spalten rausnehmen, dann ist der aus der id_rxr bestehende Teil der 2.ten Faktor-Matrix schon mal klar und für den Rest ein LGS ansetzen. Ist aber wohl nur in speziellen (handgerechneten) Fällen praktikabel.

Hab zu dem Verfahren aber nix weiter gefunden - deshalb die Frage ob du einen besseren Algorithmus (möglichst codebar, stabil) dafür hast.

@Colin

Ja, die SVD zieht sich

https://www.geogebra.org/m/j5tnapem

viel Raum dafür was falsch zu machen - insbesondere, weil in den Beispielrechnungen sich die Singulärwerte immer gleich dort befinden, wo sie hin sollen ;-)

Danke für für die Antworten - frohe Ostern...

---

@wächter

suchst du generell nach  Verfahren zur Berechnung der Pseudoinversen oder ging es nur um den Fall der Rangfaktorisierung um die geeigneten Matrizen zu finden?

---

Es ging mir speziell um die Faktorisierung, weil in Wikipedia nicht näher auf das Verfahren eingegangen wurde und ich nix dazu gefunden habe.

Und die Umsetzung unter Berücksichtigung von den speziellen Eigenheiten von ggb-CAS...