Hallo,
Ich verstehe nicht ganz, wie ich vorgehen soll.
Nun - wenn Du gar nicht weißt, was Du tun sollst, so könntest Du zumindest das Dreieck mal zeichnen und die Winkel schlicht ausmessen. Sieht so aus:
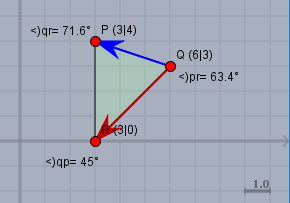
Ist zwar keine Lösung, aber eine gute Kontrolle, wenn Du eine vermeintliche Lösung errechnest. Beim Zeichnen kann Dir dann auffallen, dass die Seite \(RP\) senkrecht steht und die Seite \(RQ\) genau diagonal durch das Kästchenpapier verläuft. Der geübte Zeichner (man kann gar nicht genug solche Bildchen zeichnen!) weiß dann bereits, dass der Winkel beim Punkt \(R\) \(=45°\) sein muss!
Und wenn Du gar nichts vom Skalarprodukt weißt und die Lösung, die Silvia Dir hier geliefert hat, auch nicht verstanden hast (frage dann immer nach), dann hast Du trotzdem schon mal etwas von Winkeln im rechtwinkligen Dreieck gehört.
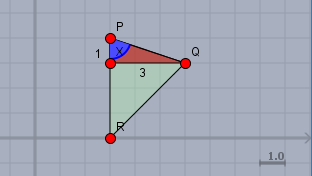
Oben siehst Du ein rechtwinkliges Dreieck \(\triangle PXQ\) und für den blau markierten Winkel \(\alpha\) beim Punkt \(P\) gilt: Tangens von \(\alpha\) ist Gegenkathete (\(|XQ|\)) zu Ankathete (\(|PX|\))$$\tan \alpha = \frac{3}{1} \implies \alpha = \arctan 3 \approx 71,57°$$Beliebige Winkel - z.B. den beim Punkt \(Q\) - rechnet man mit den anliegenden Vektoren aus. Der Vektor \(\vec{QR}\) (rot markiert s. Bild oben), der von \(Q\) nach \(R\) geht ist$$\vec{QR} = R - Q = \begin{pmatrix}3\\ 0\end{pmatrix} - \begin{pmatrix}6\\ 3\end{pmatrix} = \begin{pmatrix}-3\\ -3\end{pmatrix}$$ und der Vektor \(\vec{QP}\) (blau) ist$$\vec{QP} = P - Q = \begin{pmatrix}3\\ 4\end{pmatrix} - \begin{pmatrix}6\\ 3\end{pmatrix}= \begin{pmatrix}-3\\ 1\end{pmatrix}$$Du kannst das Ergebnis dieser Berechnung direkt in der Zeichnung überprüfen. Zeige mit einem Bleistift auf den Punk \(Q\) und gehe 3 Kästchen nach links (links, weil negativ) und 1 Kästchen nach oben. Dann muss der Bleistift bei \(P\) stehen. Der Vektor \(\vec{QP}\) ist also \(\vec{QP} = (-3\,| 1)\).
Der Winkel \(\gamma\) zwischen diesen beiden Vektoren berechnet sich aus dem Skalarprodukt. Es gilt$$\vec{QR} \cdot \vec{QP} = |\vec{QR} | \cdot |\vec{QP} | \cdot \cos \gamma$$Daraus folgt:$$\begin{aligned} \cos \gamma &= \frac{\vec{QR} \cdot \vec{QP}}{ |\vec{QR} | \cdot |\vec{QP} |} \\ &= \frac{\begin{pmatrix}-3\\ -3\end{pmatrix} \cdot \begin{pmatrix}-3\\ 1\end{pmatrix}}{\sqrt{(-3)^2 + (-3)^2} \cdot \sqrt{(-3)^2 + 1^2}} \\ &= \frac{(-3)\cdot(-3) + (-3)\cdot 1}{\sqrt{18} \cdot \sqrt{10} } \\ &= \frac{6}{6 \sqrt{5}} \\ &= \frac 1{\sqrt 5} \\ \implies \gamma &= \arccos\left(\frac 1{\sqrt 5} \right) \approx 63,43°\end{aligned}$$... und alle anderen Winkel kann man natürlich auch so berechnen.
Bleibt noch zu erwähnen, dass die Winkelsumme in einem Dreieck immer \(180°\) ist und wenn man zwei Winkel kennt ist der dritte dann die Differenz der Summe der beiden zu \(180°\).