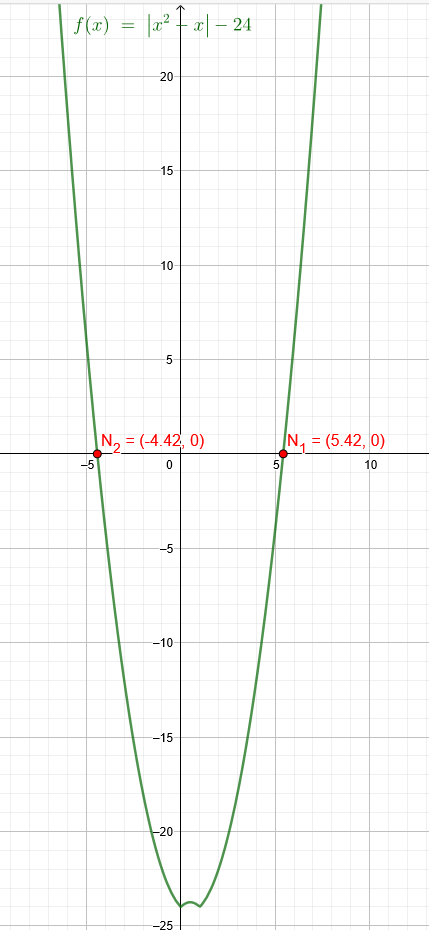
|x^2 -x| = 24
\( \left|x^{2}-x\right|=24 \)
\( \sqrt{\left(x^{2}-x\right)^{2}}=\left.24\right|^{2} \)
\( \left(x^{2}-x\right)^{2}-24^{2}=0 \)
\( \left[x^{2}-x+24\right] \cdot\left[x^{2}-x-24\right]=0 \)
\( x^{2}-x+24=0 \rightarrow \) keine Lösungen in \( \mathbb{R} \)
\( x^{2}-1 x=24 \)
\( (x-0,5)^{2}=24,25 \mid \sqrt{ } \)
1. \( ) x-0,5=\sqrt{24,25} \)
\( x_{1}=0,5+\sqrt{24,25} \approx 5,42 \)
2. \( ) x-0,5=\sqrt{24,25} \)
\( x_{2}=0,5-\sqrt{24,25} \approx-4,42 \)