Aufgabe:
Gegeben seien die Punkte \( A=(-2 ; 1), B=(3 ; 4) \) und \( C=(4 ; 2) . \)
\( \vec{u}=\overrightarrow{B A}, \vec{v}=\overrightarrow{B C} \) und \( \vec{w}=\overrightarrow{B A}+\overrightarrow{B C} \)
1) Berechnen Sie die Koordinaten des Vektors \( \vec{u} \)
2) Berechnen Sie \( 2 \vec{v}-\vec{u} . \)
3) Berechnen Sie die Länge des Vektors \( \vec{v} \)
Problem/Ansatz:
1) \(B\begin{pmatrix} 3\\4 \end{pmatrix}+A\begin{pmatrix} -2\\1 \end{pmatrix}=BA\begin{pmatrix} 1\\5 \end{pmatrix}\)
2) \(2*\vec{v}-\vec{u}=2*(B+C)-(B+A)=2*(B\begin{pmatrix} 3\\4 \end{pmatrix}+C\begin{pmatrix} 4\\2 \end{pmatrix})-(B\begin{pmatrix} 3\\4 \end{pmatrix}+A\begin{pmatrix} -2\\1 \end{pmatrix})=\begin{pmatrix} 13\\7 \end{pmatrix}\)
3)
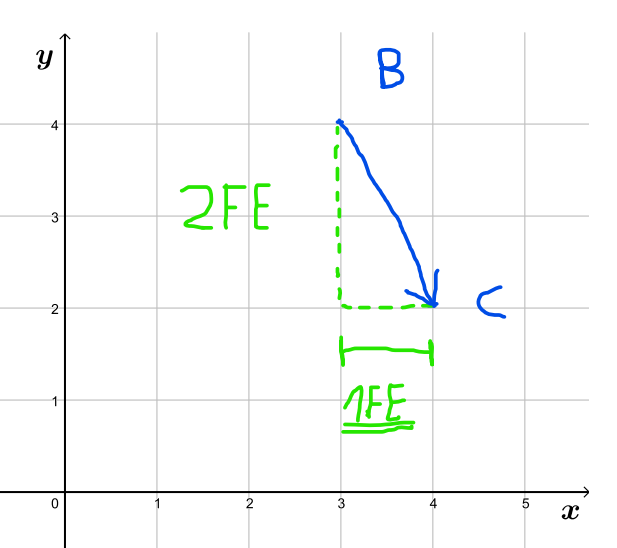
Hier würde ich jetzt diese Formel nutzen= \(a^{2}+b^{2}=c^{2}\)
\(1^{2}+2^{2}=3^{2} | \sqrt{}\)
\(3 FE=c \)
Habe ich das soweit richtig gemacht? Bin mir vorallem bei der 1 und 2 nicht so ganz sicher.