Welche der untenstehenden Aussagen bzgl. der Fixpunktiteration ist korrekt?

Question

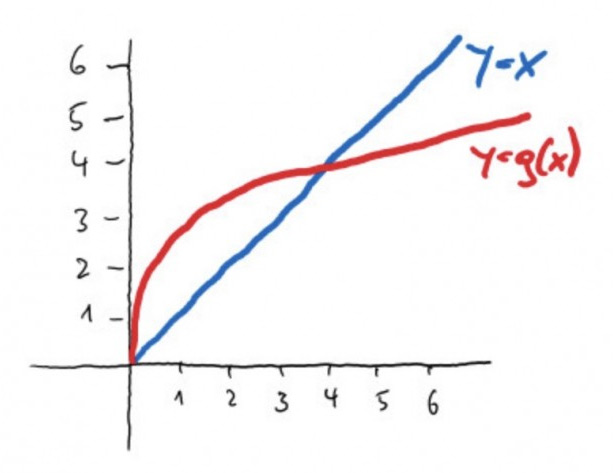
Wie in der Skizze zu sehen schneiden sich die Kurven $y=x$ und $y=g(x)$ in $x=0$ und $x=4$ Welche der untenstehenden Aussagen bzgl. der Fixpunktiteration $x_{k+1}=g\left(x_{k}\right)$ ist korrekt?

(A) Falls $\mathrm{x}_{0}=2$, dann konvergiert $\mathrm{x}_{\mathrm{k}}$ gegen $4 .$

(B) Falls $\mathrm{x}_{0}=1$, dann konvergiert $\mathrm{x}_{\mathrm{k}}$ gegen 0 .

(C) Falls $x_{0}=6,$ dann konvergiert $x_{k}$ gegen 4

Ich bin mir ziemlich sicher dass falls x₀ = 2 x_k gegen 4 konvergiert.

Kann mir jemand sagen ob ich richtig dabei liege dass sonst noch richtig ist dass c) Falls x₀ = 6 dann konvergiert x_k gegen 4 richtig ist oder?

Comments

Hallo,

Deine Antwort zu (B) ist falsch

Gruß

Answer 1

Falls x0 = 6 dann konvergiert xk gegen 4.

Ja, das passt auch.