Flächeninhalt Umkreismittelpunkt berechnen

Question

Aufgabe:

Das Dreieck ABC ist gleichschenklig mit der Basis [BC]. Es gilt: A(-3/-2); B(2/-1); BC =6 LE.

a) Zeichne das Dreieck ABC und berechne dessen Innenwinkelmaße. [Teilergebnis: α=72,06°].

b) Berechne den Flächeninhalt des Dreiecks ABC.

c) Der Punkt M ist der Mittelpunkt des Umkreises k des Dreiecks ABC. Zeichne M und k ein.

d) Zeige durch Rechnung, dass für die Mittelsenkrechte m_[AB] gilt: y= -5x-4.

e) Zeichne die Gerade g = AM und zeige durch Rechnung, dass sie folgende Gleichung besitzt: y=1,09x+1,27

f) Berechne die Koordinaten des Umkreismittelpunktes M. [Ergebnis: M(-0,87/0,35)]

g) Berechne den prozentualen Anteil des Flächeninhalts des Dreiecks ABC am Flächeninhalt des Kreises.

Problem/Ansatz:

wir haben eine Hausaufgabe aufbekommen, bei der ich leider nicht weiterkomme. Ich verstehe nicht, wie es gehen soll, dass die Seite BC die Basis sein soll, wenn es sich hierbei um ein gleichschenkliges Dreieck handelt. Da ich wahrscheinlich die Zeichnung falsch gemacht habe, bekomme ich auch andere Ergebnisse für Innenwinkelmaße und Umkreismittelpunkt als im Buch angegeben. Könnte mir jemand bei der Lösung von dieser Aufgabe helfen? Wenn es geht, bitte mit der Zeichnung auch. Vielen Dank!

Comments

Vielleicht hilft dir schon mal die Zeichnung.

mfG

Moliets

---

Vielen Dank schon mal, und könnten Sie vielleicht die Rechenschritte zu den Teilaufgaben wie z.B. Umkreismittelpunkt bestimmt wird, erklären?

---

Umkreismittelpunkt:

Eine Linie hast du schon in der Mittelsenkrechten der Strecke A B.

Nun bestimme die Mittelsenkrechte der Strecke BC. Der Schnittpunkt beider Geraden ist der Mittelpunkt des Umkreises.

mfG

Moliets

---

Vielen Dank, aber ich bin jetzt etwas durcheinander...verstehe leider nichts mehr.  Ich glaube, ich frage meine Mitschüler, ob mir jemand das erklären kann.

Danke für Ihre Lösungsansätze!

---

Ich habe aus Versehen die Strecke A B als Basis angesehen. Entschuldigung!

mfG

Moliets

Answer 1

Hallo David,

anbei eine Zeichnung:

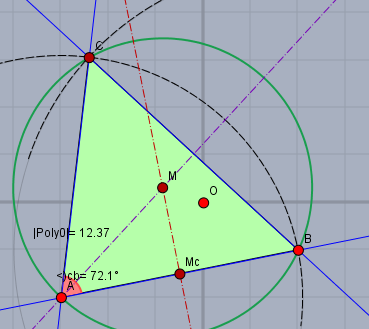
b) Berechne den Flächeninhalt des Dreiecks ABC.

Zur 'Berechnung' der Dreiecksfläche muss natürlich der Punkt $C$ berechnet werden. ich unterstelle, es soll sich um eine rechtsdrehendes Dreieck handeln, dann kann man sich auf eine von zwei Lösungen konzentrieren. $C$ ist der Schnittpunkt zweier Kreise. Ein Kreis $k_1$  um den Punkt $A$ mit dem Radius $|AB|=\sqrt{26}$ und ein Kreis $k_2$ um $B$ mit dem Radius $|BC|=6$.$$k_1: \quad (x+3)^2 + (y+2)^2 = 26 \\ k_2: \quad (x-2)^2 + (y+1)^2 = 6^2 \\ \begin{aligned} 6x + 9 + 4y + 4 - (-4x + 4 + 2y + 1) &= 26 - 36 &&\left|\, k_1 - k_2 \right.\\ 10x +2y &= -18 \\ 5x + y &= -9 \implies y = -5x -9 \\ (x-2)^2 + (-5x -9+1)^2 &= 6^2 \\ x^2 - 4x + 4 + 25x^2 + 80x + 64 &= 36 \\ 26x^2 + 76x + 32 &= 0 \end{aligned} \\ \begin{aligned} x_{1,2} &= \frac{-76 - \sqrt{ 76^2 - 4\cdot 26 \cdot 32 }}{2\cdot 26} \\ &= \frac{-19 \pm \sqrt{153}}{13} \approx -2,41 \\ \implies y &= \frac{-22 + 5\sqrt{153} }{13} \approx 3,07 \end{aligned}$$Ein Trick besteht darin, die beiden Kreisgeichungen zunächst von einander abzuziehen. Und anschließend das Resultat in einer der beiden Kreisgleichungen einzusetzen. Dann bekommt man immer eine quadratische Gleichung. Und ich habe die zweite Lösung gleich weg gelassen. Also ist $C\approx (-2,41|\,3,07)$.

Den Flächeinhalt $F$ berechnet man bei Kenntniss der drei Koordinaten des Dreiecks am einfachsten mit dem 'Kreuzprodukt'$$F = \frac 12 \vec{AB} \times \vec{AC} = \frac 12 \begin{pmatrix}5\\ 1\end{pmatrix} \times \frac 1{13} \begin{pmatrix}20 - \sqrt{153}\\ 4 +5\sqrt{153 }\end{pmatrix} \\ \quad = \sqrt{153} \approx 12,37$$

d) Zeige durch Rechnung, dass für die Mittelsenkrechte m[AB] gilt: y= -5x-4.

Der Normalenvektor $\vec n$ der Mittelsenkrechten ist $\vec{AB}$ (s.o.) $m_{AB}$ verläuft durch den Mittelpunkt der Strecke $AB$, Also kann man direkt die Normalform aufstellen:$$\begin{aligned} \vec n \cdot \vec x &= \vec n \cdot \frac 12 (A + B)\\ \begin{pmatrix}5\\ 1\end{pmatrix} \vec x &= \begin{pmatrix}5\\ 1\end{pmatrix} \cdot \frac 12 \left( \begin{pmatrix}-3\\ -2\end{pmatrix} + \begin{pmatrix}2\\ -1\end{pmatrix}\right) \\ 5x + y &= -4 \\ y &= -5x -4 \end{aligned}$$

e) Zeichne die Gerade g = AM und zeige durch Rechnung, dass sie folgende Gleichung besitzt: y=1,09x+1,27

$AM$ ist die Mittelsenkrechte über der Strecke $BC$. Der Normalenvektor ist $BC$ und sie geht durch die Mitte der Strecke $BC$ - also durch $(B+C)/2$. Rechne mal selber ... ich habe $$y = 1,086 x + 1,257$$

f) Berechne die Koordinaten des Umkreismittelpunktes M.

Ist der Schnittpunkt der beiden Geraden - also die Lösung des LGS$$\begin{aligned} y &= -5x -4 \\ y &= 1,086 x + 1,257\end{aligned}$$mit der Lösung $M=(-0,864|\, 0,319)$ (Deine Lösung ist wahrscheinlich falsch gerundet!)

g) Berechne den prozentualen Anteil des Flächeninhalts des Dreiecks ABC am Flächeninhalt des Kreises.

schaffst Du das alleine ? Tipp: der Radius des Umkreises ist $|MA|$

Falls Du Fragen hast, so melde Dich bitte.

Gruß Werner

Comments

Es ist sehr, sehr nett und freundlich von Ihnen, herzlichen Dank für ausführliche Lösungen Herr Werner-Salomon!

Darf ich fragen, sind Sie vielleicht ein Mathe-Lehrer? Ich wünschte mir, ich könnte auch so gut Mathe verstehen...DANKE!!!

---

Und bei der Teilaufgabe g) muss man wahrscheinlich den Kreisumfang und Dreiecksumfang bestimmen, dann entspricht der Kreisumfang 100% und vom Dreieck x% und nach x auflösen. Auf jeden Fall geht es hier um Kreisumfang oder?

---

sind Sie vielleicht ein Mathe-Lehrer?

Nein - ich bin weder Mathe-Lehrer, noch habe ich Mathematik studiert. Ich bin Ingenieur und ohne die Mathekenntnisse könnte ich meinen Beruf nicht so ausführen, wie ich es tue.

Ich wünschte mir, ich könnte auch so gut Mathe verstehen

Wenn Du es - bzw. mehr - lernen willst, so musst Du es selber tun! Das ist wie Fahrrad fahren. Das lernt man nicht durch zusehen. Genauso wenig lernst Du Mathe, indem ich Dir hier die Aufgaben vorrechne,

Du musst sie selber rechnen. Zumindest erstmal nachrechnen und verstehen, was Du da rechnest und warum. Und frage nie nach der Formel, sondern versuche zu verstehen und frage nach dem logischen Zusammenhang.

Und bei der Teilaufgabe g) muss man wahrscheinlich den Kreisumfang und Dreiecksumfang bestimmen

Es ist nicht nach dem Verhältnissen der Umfänge, sondern nach dem Verhältnis der Flächen gefragt. Die Fläche des Dreiecks ist ja bereits berechnet worden (siehe b)). Dann fehlt noch die Fläche des Umkreises. Diese entspräche dann der 100%.

Answer 2

Zunächst ist festzustellen, dass es 2 solche Dreiecke gibt.

Die Länge AB berechnet sich nach Pythagoras als |AB|=√26. Dann ist die Höhe auf BC wiederum nach Pythagoras √17.

a) Ein Innenwinkel α (Basiswinkel) berechnet sich zum Beispiel als tan(α)=√17/3.Ein zweiter ist genau so groß und ein dritter ist 180°-2α.

b) Der Flächeninhalt ist 3√17.

Comments

Ich danke Ihnen auch vielmals Herr Roland!