Zeige: Es existiert genau ein p_{0} € ℝ² und bestimmen von Umkreismittelpunkt

Question

Aufgabe:

1) Gegeben seien drei Punkte \( a, b, c \in \mathbb{R}^{2}, \) die nicht auf einer gemeinsamen Geraden liegen. Zeige: Es existiert genau ein \( p_{0} \in \mathbb{R}^{2} \) mit \( \left\|a-p_{0}\right\|_{2}=\left\|b-p_{0}\right\|_{2}=\left\|c-p_{0}\right\|_{2} \) und es gilt
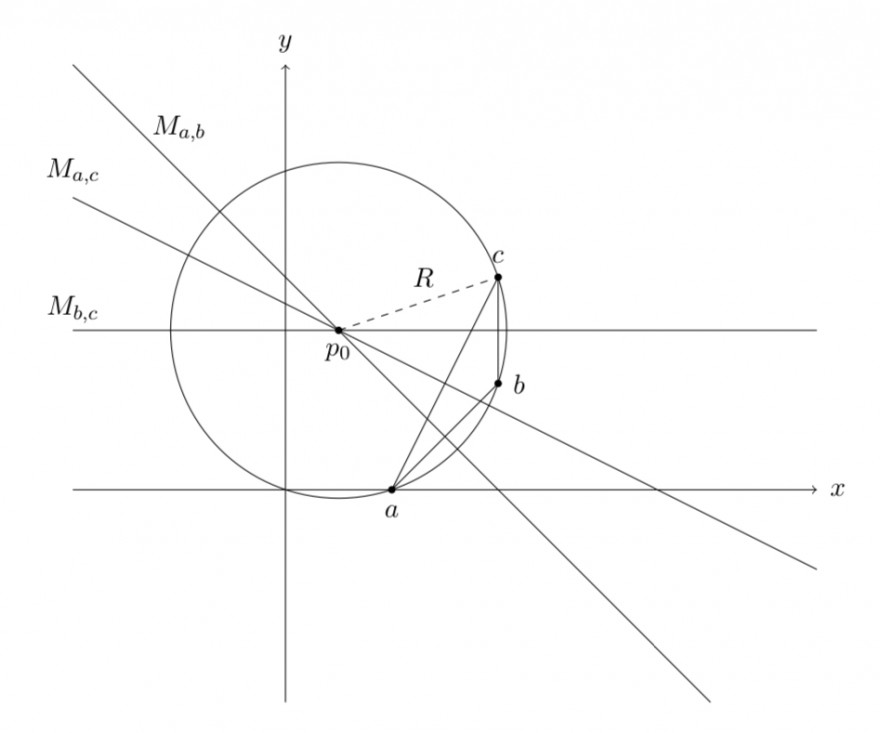
$$ M_{a, b} \cap M_{b, c} \cap M_{a, c}=\left\{p_{0}\right\} $$

Die Mittelsenkrechten schneiden sich also im Umkreismittelpunkt \( p_{0} \) des Dreiecks \( \Delta(a, b, c) . \) Der \( U \) mkreisradius ist dann \( R=\left\|a-p_{0}\right\|_{2} \)

2) Nun seien $$ a=\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \quad b=\left(\begin{array}{l} 2 \\ 1 \end{array}\right) \quad c=\left(\begin{array}{l} 2 \\ 2 \end{array}\right) $$

Bestimme Umkreismittelpunkt und Umkreisradius des Dreiecks \( \Delta(a, b, c) \)

Mittelsenkrechten schneiden sich im Umkreismittelpunkt

Answer 1

\(M_{a, b} \cap M_{b, c} \cap M_{a, c}\)

Parameterdarstellung von \(M_{a,b}\) und \(M_{b,c}\) gleichsetzen. Das hast du bestimmt schon in der Schule so gemacht. Das ist hier nichts anderes.

Anschließend Punktprobe ob der Schnittpunkt auch auf der Geraden \(M_{a,c}\) liegt.

\(\left\|a-p_{0}\right\|_{2}=\left\|b-p_{0}\right\|_{2}=\left\|c-p_{0}\right\|_{2}\)

Den gefundenen Punkt einsetzen. Eindeutigkeit folgt aus der Eigenschaft der Mittelsenkrechten.

Comments

Könnte ich bitte einen Lösungsansatz bekommen?