Question

Die Flugbahn einer Kugel kann annähernd durch eine quadratische Funktion beschrieben werden

y=b1+b2⋅x+b3⋅x2,
wobei x die zurückgelegten Meter der Kugel, y die Höhe der Kugel in Metern, und b1,b2,b3 die Parameter der Kugel bezeichnen.

Es liegen folgende vier empirische Messungen vor:

xi 3      9     13    18
yi 63  138  158  139
a. Ermitteln Sie den Parameter b1 der Flugbahn.
b. Ermitteln Sie den Parameter b2 der Flugbahn.
c. Ermitteln Sie den Parameter b3 der Flugbahn.
d. Welche Flughöhe erreicht die Kugel nach 20 Metern?
e. In welcher Entfernung trifft die Kugel auf dem Boden auf?

Answer 1

Hallo

Lösungen aus der Wertabelle in die Funktiongleichung einsetzen

3| 63        63 = b1+ b2*3 +b3*3²

9| 138      138 =b1+b2*9+b3* 138²

13|158      158 =b1+b2*13+b3*13²

3 unbekannte 3 Gleichungen, löse das System

d) 20 = x indie gefunden Funktion eingeben

e) Nullstellen finden

Comments

Beachte das 4 Punkte gegeben waren und damit ein Interpolations-Polynom gesucht ist.

---

a) 5.25

b)21,5

c)-0,75

d)135,25

e)28,91

habe diese Lösungen herausbekommen aber leider habe ich etwas falsch...können Sie mir vielleicht helfen?

Answer 2

[Rechnung versteckt]

b3 = -0.8524530032 ∧ b2 = 23.02081613 ∧ b1 = 1.271251719

f(20) = 120.7063730

f(x) = 0 --> x = 27.06048802

Comments

Hallo, danke für Ihre Antwort...aber wei sind sie auf b1 b2 und b3 gekommen? Ich habe da ganz andere Lösungen.

---

Bin jetzt auf die gleichen Lösungen wie Sie gekommen. Sind die nun richtig? Denn ich habe leider nur mehr einen Versuch:)

---

Ich bin mir zu 99% sicher, dass meine Antworten stimmen. Aber du kannst das gerne zur Sicherheit nachrechnen.

---

Also wie ich jetzt mitbekommen habe sind die Lösungen von Der_Mathecoach richtig oder? :)

---

Die sind richtig.

mfG

Moliets

---

Hallo, wie sind Sie auf b1, b2 und b3 gekommen? :)

---

Da gibt es im internet einen eigenen rechner... Per hand lösen weiß ich allerdings auch nicht wie das geht :/

---

hab einen gefunden, weiß aber nicht wie ich es genau eingeben muss, bekomme immer andere Ergebnisse.

---

Danke, hab das Ergebnis jetzt!

---

wie hast dus gelöst?

---

Eine Ausgleichsparabel für 4 Punkte zu
Fuß zu berechnen ist zuviel Arbeit.
Im Internet gibt es Rechner die dir
diese Arbeit abnehmen können.
Bei Bedarf nachfragen.

Answer 3

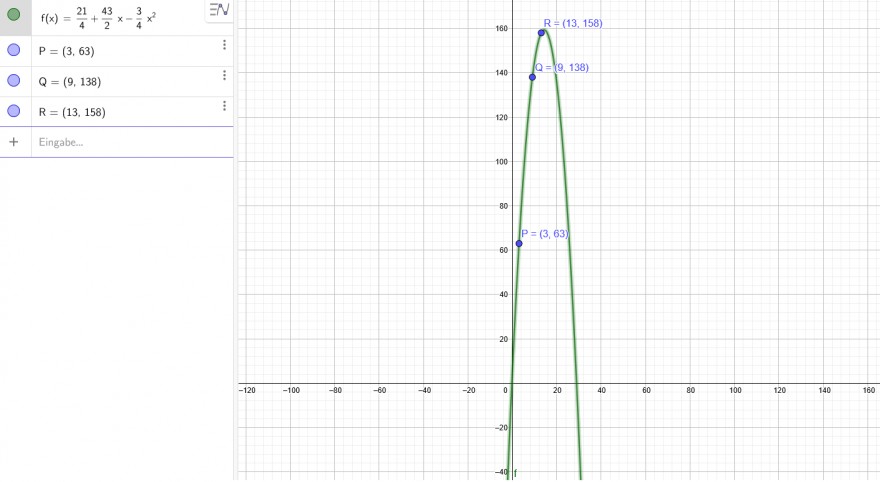
y(x)  = b1 + b2⋅x+ b3⋅x^2

xi    3      9     13     18
yi 63  138   158   139

P( 3| 63 )

y(3)  = b_1 + 3*b_2+ 9 *b_3

1.)  b_1 + 3*b_2+ 9 *b_3 = 63

Q( 9| 138 )

y(9)  = b_1 + 9*b_2+ 81 *b_3 

2.)  b_1 + 9*b_2+ 81 *b_3 =138

R( 13| 158 )

y(9)  = b_1 + 13*b_2+ 169 *b_3

3.)  b_1 + 13*b_2+ 169 *b_3 =158

b_1 =      \( \frac{21}{4} \)

b_2=      \( \frac{43}{2} \)

b_3=      - \( \frac{3}{4} \)

y(x)  = \( \frac{21}{4} \)  +  \( \frac{43}{2} \)   x   - \( \frac{3}{4} \)  x^2

mfG

Moliets

Comments

DIe Lösungen bei b1, b2 und b3 habe ich auch so herausbekommen und habe sie so eingegeben.
Bei d) habe ich 135,25 herausbekommen und bei e) habe ich 28,91...allerdings ist bei den Lösungen etwas falsch..

könnten Sie mir bitte weiterhelfen?