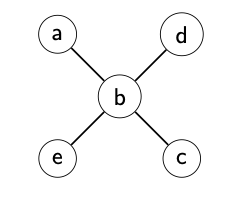
Im Mathematikunterricht der Grundschule werden sogenannte "Zauber-Xe" eingesetzt. Ihre Grundstruktur ist der nebenstehenden Abbildung zu entnehmen. Die Werte der Zahlen \( a, b, c, d \) und \( e \) dürfen beliebige reelle Zahlen sein. Maßgebend ist, dass für ein , Zauber-X" gelten muss:
$$ a+b+c=b+d+e $$
Zeige :
(i) Für beliebige , Zauber-Xe" \( A \) und \( B \) ist stets auch \( A+B \) ein , Zauber- \( \mathrm{X} \) ".
(ii) Für jedes "Zauber- \( \mathrm{X}^{\prime \prime} A \) und jede reelle Zahl \( \lambda \) ist auch \( \lambda \cdot A \) ein \( _{n} \) Zauber- \( \mathrm{X}^{\prime \prime} \)