Kepler Potential, Kurvendiskussion durchführen?

Question

ich muss die Bewegung im Kepler-Potential hier betrachten
$U(r)=-\frac{k}{r}, \quad k>0$
Plotten Sie das in Gleichung (136) im Skript definierte effektive Potential $V_{L}(r)$ für verschiedene Werte des Drehimpulses $L .$

Zudem muss ich diskutieren, ob es lokale Minima, lokale Maxima oder Sattelpunkte gibt und welche Art von Orbits durch das Auftreten dieser Extremwerte angezeigt wird.
Wisst ihr, wie ich hier vorzugehen habe?

Gleichung (136): $V_{L}(r)=U(r)+\frac{L^{2}}{2 m r^{2}}$

Answer 1

Die Gesamtenergie beträgt $$E = T + V$$ wobei $T$ die kinetische Energie ist und $$T(t) = \frac{m}{2} \dot r^2(t)$$ beträgt. Daraus ergibt sich $$\dot r^2(t) = \frac{2}{m} \bigg( E - V(r) \bigg)$$

Wenn jetzt $E < V(r)$ ist, gibt es keine Lösungen und entspricht demzufolge keiner physikalisch erlaubten Lösung des Kepplerproblems. Ist $V < E < 0$ gibt es zwei Lösungen, die der Lösung $E = V$ entsprechen. Ich habe hier ein Beispielplot gewählt um das mal darzustellen.

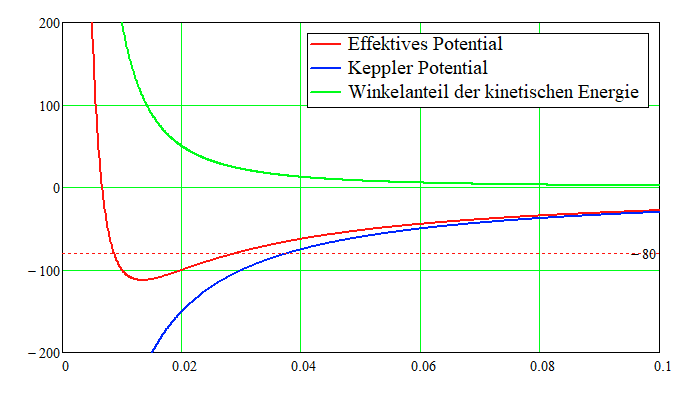
Wenn $E = V$ ist, gibt es genau eine Lösung für $\dot r$, also $\dot r = \text{ const }$ und das ist dann eine Kreisbewegung.

Wenn $E > 0$ ist, dann gibt es nur eine Lösung von $E = V$ und $\dot r^2$ bleibt $\gt 0$

Damit liegt eine ungebundene Bewegung vor.

Comments

Super, ich danke dir!