Wie berechnet man die Abzissenschnittpunkte mit Hilfe dieser Funktionen?

Question

Aufgabe:

y=(x-3)²-1

y=4(x-3)²-1

Wie berechnet man die Abzissenschnittpunkte mit Hilfe dieser Funktionen?

Problem/Ansatz:

Answer 1

1.) y=(x-3)²-1

(x-3)²-1=0

(x-3)²=1

1.)  x-3=$\sqrt{1}$=1

x₁ = 4

2.)  x-3= - $\sqrt{1}$=-1

x₂ = 2

2.) y=4*(x-3)²-1

4*(x-3)²  - 1=0  |+1

4*(x-3)²  = 1| :4

u.s.w.

mfG

Moliets

Comments

Kannst du mir 4(x-3)²-1 nochmal erklären? Ich rechne ÷4 dann kommt ja 1 raus,also 1x +9=1?

---

4*(x-3)²  = 1| :4

(x-3)²  = $\frac{1}{4}$

1.) x - 3=   1/4^(1/2)  = $\frac{1}{2}$

x₁ =3+ $\frac{1}{2}$=  $\frac{7}{2}$

x₂=  3 - $\frac{1}{2}$ =  $\frac{5}{2}$

mfG

Moliets

Text erkannt:

$f(x)=4(x-3)^{2}-1$
$=R$

---

Wie kommt man auf 1/2 und wieso ist 3 + 1/2 =7/2?

Y=(x-2)²-1

Y=-(x+1)²+2

Y=-2(x-2)+1

Y=(x-2)²+1

Ich soll von diesen Funktionen denn abzissenschnittpunkt ausrechnen aber ich bin zu unterbelichtet das hinzubekommen,obwohl es wahrscheinlich für euch ziemlich einfach ist

---

" Wie kommt man auf 1/2 und wieso ist 3 + 1/2 =7/2?"

Die Quadratwurzel aus $\frac{1}{4}$ ist $\frac{1}{2}$, weil $\frac{1}{2}$•$\frac{1}{2}$=$\frac{1}{4}$ ist.

3 + $\frac{1}{2}$ = $\frac{7}{2}$ →

3=$\frac{6}{2}$

$\frac{6}{2}$ + $\frac{1}{2}$= $\frac{7}{2}$

Bezüglich der Nullstellen der weiteren Funktionen empfehle ich dir, die gegebenen Lösungen eigenständig durchzurechnen und bei Bedarf auf den Lösungsweg zu schauen.

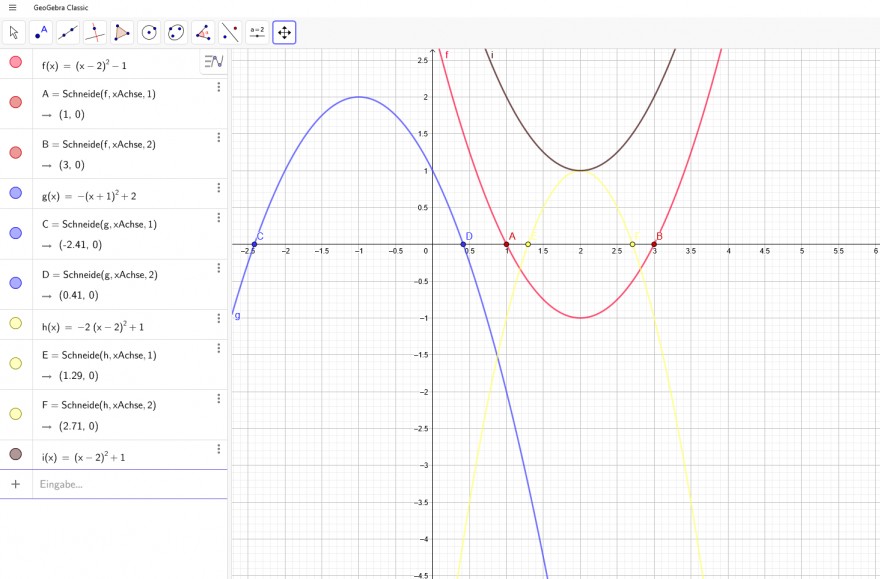
Zur Kontrolle der Nullstellen:

f(x)= (x - 2 )² - 1 → in rot

g(x)= - ( x +1 ) ² + 2→ in blau

h(x)=-2(x-2)²+1→ in gelb

i(x)=  (x - 2 )² + 1→ in schwarz → keine Lösung im reellen Bereich!

mfG

Moliets

Text erkannt:

6
$f(x)=(x-2)^{2}-1$
$A=$ Schneide(f, xAchse, 1$)$
$\rightarrow(1,0)$
$B=$ Schneide(f, xAchse,2)
$\rightarrow(3,0)$
$g(x)=-(x+1)^{2}+2$
$c=$ Schneide(g, xAchse, 1 ) $\rightarrow(-2.41,0)$
$\mathrm{D}=$ Schneide( $\mathrm{g},$ xAchse, $, 2)$
$\rightarrow(0.41,0)$
$h(x)=-2(x-2)^{2}+1$
$E=$ Schneide(h, xAchse, 1 ) $\rightarrow(1.29,0)$
$F=$ Schneide(h, xAchse, 2 )

Answer 2

Das sind die Schnittpunkte mit der x-Achse.

also:    (x-3)²-1  =0

         (x-3)²  =  1

   x-3 = 1    oder   x-3 = -1

        x=4    oder   x = 2

==>  Abszissenschnittpunkte (4;0)  und (2;0) .