Vom Duplikat:
Titel: Errorfunktion, Konstanten berechnen, welchen Fehler begehe ich
Stichworte: differentialgleichungen,konstante,gleichungen
Aufgabe:
genaue Berechnung der Konstanten der Errorfunktion
Problem/Ansatz:
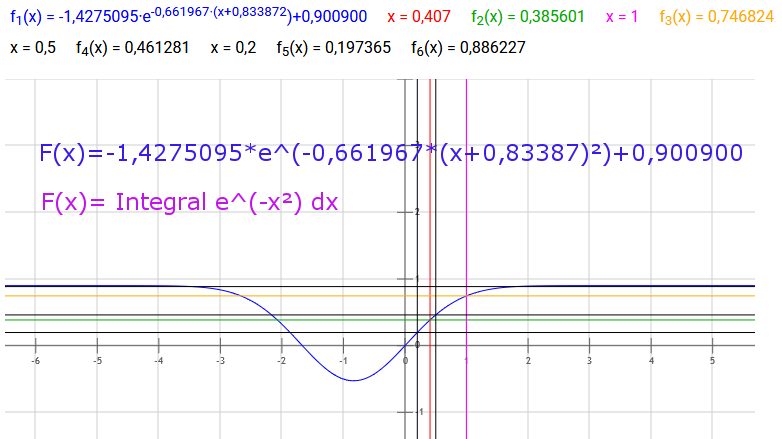
F(x)=-a*e^(-b*(x+c)^2)+d
Diese Konstanten sollen berechnet werden!
Berechnung von b:
F(x)=-a*e^(-b*(x+c)^2)+d=∫e^(-x^2) dx
1.Ableitung: f'(x)=2ab(x+c)*e^(-b(*x+c)^2)=e^(-x^2)
2.Ableitung: f''(x)=-2ab*(2b*(x+c)^2-1)*e^(-b*(x+c)^2)=-2x*e^(-x^2)
2. Ableitung Umstellen und Gleichsetzen mit 1. Ableitung ergibt für b:
b=(x*(x+c)+1)/(x+c)^2
Berechnung von c:
Wendpunkt von F(x)=f''(x)=0
f''(x)=0 (x+c)^2=x^2+2xc+c^2
xw=c+1=x, dies ist richtig
Probe für c:
F(1-c)=F(c-1), F(x)=F(-x)
x=c+1 als Ergebnis
Nullstellen:
F(x)=-a*e^(-b*(x+c)^2)+d=0
-c+((-1/b)*ln(d/a))^(1/2)=x, x=0 usw., dies ist auch richtig
und jetzt kommt wahrscheinlich mein Fehler, weiß mir nicht anders zu helfen:
Berechnung von a: Bildung der beiden inversen Funktionen, diese sind im Bereich von
d-a=<x=<-1+c und -c=<y=<-1+c, geich!!!!!!
yi1=yi2
~plot~ x=-0,83382;0,900900-1,427;x=1-0,8338;x=-1,8338;0,161;0,9009;-0,36787;((-ln(-x+0,4739))^(0.5)-0,83382);x; (-1/0,6619*ln((x-0,9009)/(-1,427)))^(0,5)-0,83382;[[-1|1|-1|1]];-0,83382;x=-0,5261;x=-1+0,83382; ~plot~
Graph 5 und Graph 7 sind in dem angegebenen Bereich gleich, dies kommt dadurch, daß es ein Verhältinis der Extremwerte von y2=-e^(-x+c)^2 und y1=-a*(e^(-b*(x+c)^2))+d gibt, für beide Funktionen, eine Verhältinismäßigkeit xe=gleich für beide Funktionen, und auch xw gleich
y1(xe)/y2(xe)=(d-a)/(-1)
Wendepunkte von yiw1=yiw2 ergibt yiw2=xiw2 (!!!!!!) usw. mit einem Ergebnis für a=(c+(d-x+1)*lnx+x)/lnx und dies stimmt dann nicht......meine Frage, gibt es einen andere Möglichkeit den konstanten Faktor a zu berechnen, daran wird alles liegen....
Dankeschön für die Antworten und die Zeit der Durchsicht....! Bert Wichmann!