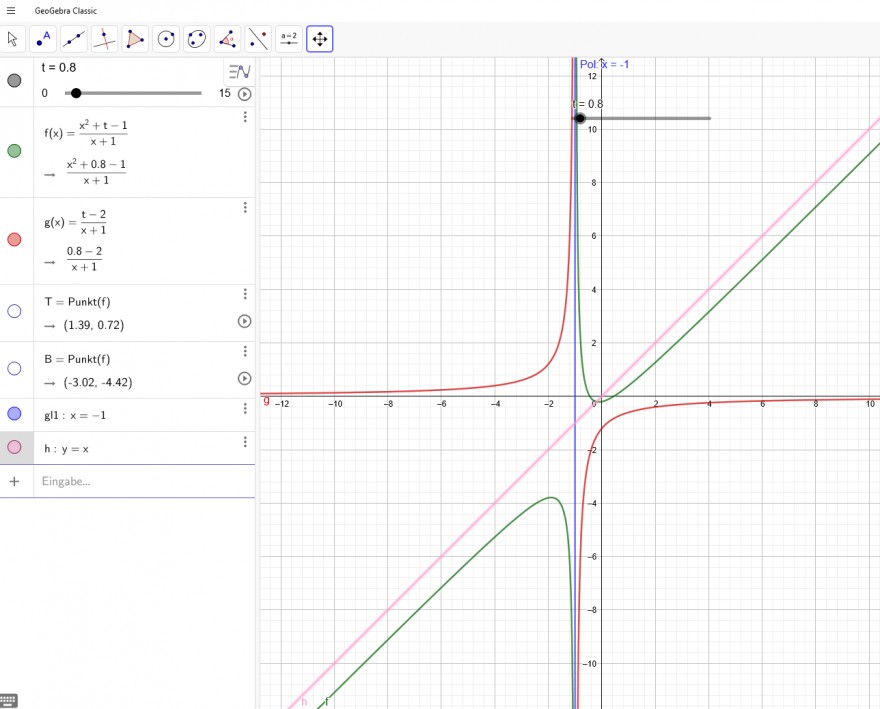
f _t(x) = \( \frac{x^2 + t -1}{x + 1} \)
1. )Wie lautet die Definitionsmenge?
Alle x außer x= - 1
2. )Wie finde ich die Nullstellen heraus?
f _t(x) =0
\( \frac{x^2 + t -1}{x + 1} \) = 0
x^2 = 1 - t
x₁ =\( \sqrt{1-t} \) wobei t nicht größer als 1 werden darf.
x₂= -\( \sqrt{1-t} \) "
3. )Wie finde ich die Polstelle raus, wenn t in der Funktion steht?
Polstelle findest du, wenn der Nenner = 0 x + 1=0 x= - 1 siehe auch 1.)
4. )Wie lautet die Asymptote
(x^2 + t - 1 ) : (x+1) = x
- (x^2 + 1)
----------------
t - 2
1. Asymptote: y=x
2. Asymptote: \( \frac{t - 2}{ x+1} \)
5.) Wie bestimme ich die Ortskurve der Tiefpunkte?
f´(x)=0
f´(x)= \( \frac{(2 x*(x+1)-(x^2+t-1))}{(x+1)^2} \) = \( \frac{x^2+2x-t+1}{(x+1)^2} \)
\( \frac{x^2+2x-t+1}{(x+1)^2} \) = 0
x^2+2x= t - 1
(x+1)^2= t - 1+1 = t
x₁ = - 1 + \( \sqrt{t} \) → f_t (x₁) = ...
x₂= - 1 - \( \sqrt{t} \) → f_t (x₂) = ...
Art des Extremwertes mit f´´(x₁) und f´´(x₂) Mit dem Wert >0 liegt ein Minimum andernfalls ein Maximum vor.
Die Ortskurve bestimmen ist noch nicht so mein Gebiet.