Lagebeziehungen prüfen, Parametervergleich

Question

Aufgabe - Prüfung von Lagebeziehungen:

Prüfen Sie, ob der Punkt P(0 0 6) auf der Geraden g durch A(2 2 4) und B(4 4 2) liegt).

Problem/Ansatz:

Ich habe schon herausgefunden, dass r=-1 ist. Jetzt muss ich einen Parametervergleich durchführen, dafür muss ich die Streckenendpunkte von A und B wissen, ich weiß aber nicht wie ich diese bestimme. Die Aufgabe hierfür lautet: Prüfen Sie, ob die Punkt P Q R auf der Geraden g durch A und B oder sogar auf der Strecke AB liegen.

Answer 1

Hallo,

..., dafür muss ich die Streckenendpunkte von A und B wissen

Die Streckenendpunkte der Strecke $AB$ sind die Punkte $A$ und $B$. Und diese sind doch gegeben.

Ich glaube, dass Dein Verständnisproblem darin liegt, dass Du nicht weißt, was die Parameterform einer Geraden aussagt. Die Parameterform der Geraden $g$ durch die Punkte $A$ und $B$ ist doch$$g: \quad \vec x = A + r \cdot (B-A) = \begin{pmatrix}2\\ 2\\ 4\end{pmatrix} + r \begin{pmatrix}2\\ 2\\ -2\end{pmatrix}$$Ist Dir klar, wofür dieses $r$ eigentlich steht?

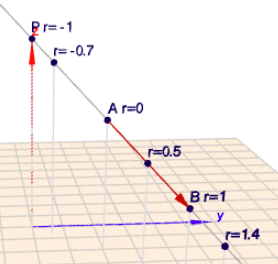
ich habe Dir oben die Gerade $g$ gezeichnet. Sowie für einige Werte von $r$ die dazugehörigen Punkte. Diese liegen natürlich alle auf der Geraden $g$. Klicke mal auf das BIld, dann öffnet sich Geoknecht3D, Du kannst die Szene mit der Maus rotieren und bekommst einen besseren räumlichen Eindruck.

Die Gerade $g$ ist die Menge aller Punkte, die man erreichen kann, indem man für das $r$ einen beliebigen Wert einsetzt. Zwei Punkte haben dabei eine 'Sonderrolle'. Den Punkt $A$ erreicht man immer mit $r=0$ und den Punkt $B$ immer mit $r=1$. Denn$$g(0): \quad \vec x(r=0) = A + 0 \cdot(B-A) = A\\ g(1): \quad \vec x(r=1) = A + 1 \cdot (B-A) = A + B -A = B$$Wenn Du also wissen möchtest, ob ein Punkt zwischen $A$ und $B$ - und damit auf der Strecke $AB$ - liegt, so muss das $r$ zwischen $0$ und $1$ liegen.

Comments

vielen lieben Dank, Verständnisproblem gelöst

Answer 2

ob der Punkt P(0 0 6) auf der Geraden g durch A(2 2 4) und B(4 4 2) liegt

Das ist genau dann der Fall, wenn die Gleichung

        $\begin{pmatrix}0\\0\\6\end{pmatrix} = \begin{pmatrix}2\\2\\4\end{pmatrix}+r\cdot\begin{pmatrix}4-2\\4-2\\2-4\end{pmatrix}$

eine Lösung hat.

ich hab schon herausgefunden, dass r=-1 ist

Das ist eine Lösung obiger Gleichung. Also liegt $P$ auf der Geraden durch $A$ und $B$.

Comments

Vielen Dank erstmal für die zügige Antwort Oswald, doch das ist nicht mein Problem, wie du auch sagst dass der Punkt P auf der Geraden liegt habe ich es auch raus, nur ist mir der Parametervergleich, wofür ich die Streckenendpunkte von A und B brauche noch nicht bewusst :)

ich werde meinen Beitrag noch präziser bearbeiten

vg