Ich verstehe es nicht ganz könnten Sie es mir etwas gründlicher erklären
Schau mal auf das Bild.

Wenn Du drauf klickst kannst Du es vergrößern und rotieren und bekommst einen besseren räumlichen Eindruck.
Das Bild soll das halbe Glas darstellen und den kürzesten (gepunkteten) Weg der Spinne zur Fliege.
Wenn man das halbe Glas dagegen abwickelt, dann sieht das so aus:
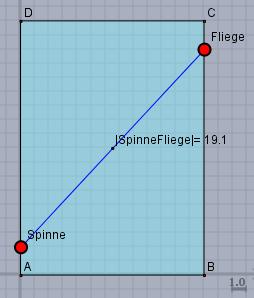
Von \(A\) bis \(B\) ist es der halbe Umfang - also 13cm. Die Höhendifferenz von Spinne zu Fliege sind \((18-2)-2=14\). Der Rest ist Pythagoras.