f(x)=-1/2 x 2+2x+2 Geradengleichung, Schnittwinkel, Tangente?

Question

Aufgabe:

a) Eine Gerade durch den Punkt P(-1/0) schneidet den Graphen von f an der Stelle x=0. Geben Sie die Geradengleichung und die Größe des Schnittwinkels an.

Problem/Ansatz:

Hallo ich habe Probleme bei der Lösung dieser Aufgabe. Ich kann die Geradengleichung nicht ganz verstehen, und die Größe des Schnittwinkels verstehe ich gar nicht. Wäre dankbar für jede Hilfe.

Answer 1

Eine Gerade durch den Punkt P(-1/0) schneidet den Graphen von f an der Stelle x=0,

also im Punkt ( 0 ; 2 )

==>  m = ( 2-0) / ( 0-(-1)) = 2      also y = 2x+2   (Geradengleichung)

Steigung von f im Punkt P ist f ' (0) = 2 also beide haben

dort die gleiche Steigung ==> Winkel = 0°.

siehe: ~plot~ -x^2/2+2x+2;2x+2 ~plot~

Answer 2

Wenn du die Geradengleichung und die Funktion f genannt hättest, hätte ich es dir konkret vorführen können. So aber nur allgemein:

Die Gerade y=mx+b hat überall die Steigung m₁. Die Funktion f hat an der Stelle x=0 die Steigung m₂=f '(0). Aus m₁ und m₂ berechnet man mit Hilfe einer Formel aus der Formelsammlung den Schnittwinkel.

Comments

Die Funktion f steht in der Überschrift, die Gerade ist ja gesucht, die weiß ich selber nicht :)

Answer 3

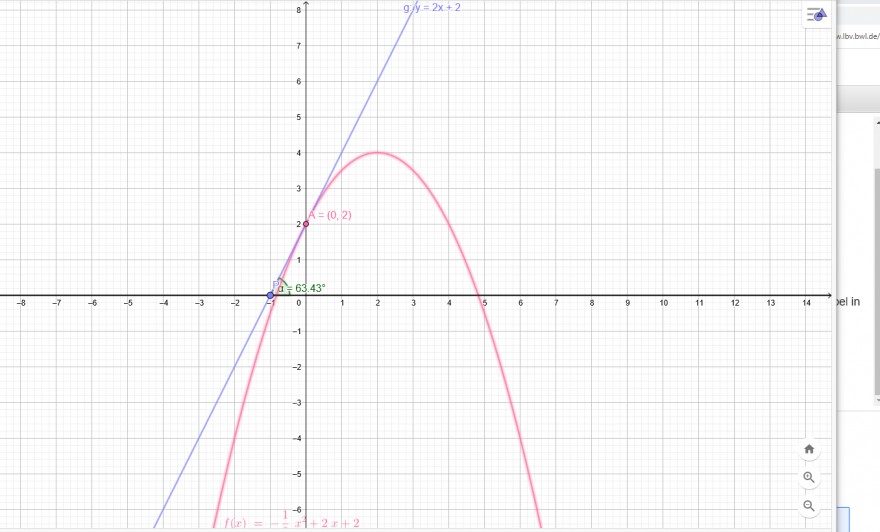
f(x)=-0,5x^2+2x+2

Geradengleichung durch P(-1|0)  und f(0)=2  →  A(0|2)

\( \frac{y_2-y_1}{x_2-x_1} \)=m  

\( \frac{2-0}{0+1} \)= 2  

y=m*x + n   mit m=2    und n=2

y=2*x + 2

Parabel mit dieser Geraden schneiden:

-0,5x^2+2x+2 = 2*x + 2

-0,5x^2 = 0

x=0   und y =2    Die Gerade schneidet die Parabel nur in einem Punkt. Sie ist somit eine Tangente der Parabel in A(0|2)

Der Schnittwinkel lässt sich nun mit der Steigung m=2  berechnen:

\( tan^{-1} \) (2)=63,43°