Hallo,
zu 1.) \(2|z| = z \cdot \overline z + 1\)
Substitution$$z=x+yi \implies |z| = \sqrt{x^2 + y^2}, \quad z \cdot \overline z = (x+yi)(x-yi)= x^2+y^2 = |z|^2$$Einsetzen in den Term aus 1) gibt dann$$\begin{aligned}2|z| &= |z|^2 + 1 \\ 0 &= |z|^2 - 2|z| + 1 \\ &= (|z|-1)^2 \\ \implies |z| &= 1\end{aligned}$$.. und das ist der Einheitskreis in der Gauß'schen Zahlenebene.
zu 2.) \(\text{Im}(z+ 1) \le \text{Re}(z -1)\)
- Wenn z=x+iy, also x=Re(z) und y=Im(z), wie ist dann |z| definiert?
(s.o..) \(|z| = \sqrt{x^2 + y^2}\) Setze einen Punkt in die Gauß'sche Zahleneben und bestimme mit Pythagoras die Entfernung zum Ursprung.
- Wenn z=x+iy, was ist dann der Realteil von z+1, was ist der Imaginärteil von z+1?
$$\text{Re}(z +1) = \text{Re}(x+yi +1) = \text{Re}((x+1)+yi) = x+1 \\ \text{Im}(z+ 1) = \text{Im}(x+yi+ 1) = \text{Im}((x+1)+yi) = y$$
- Wenn das geklärt ist, was ist dann |z+1| und dementsprechend |z+1|2?
$$|z+1| = |(x+1) + yi| = \sqrt{(x+1)^2 + y^2} \\ \implies |z+1|^2 = (x+1)^2 + y^2$$ zur Aufgabe:$$\begin{aligned}\text{Im}(z+ 1) &\le \text{Re}(z -1) &&|\, z = x+ yi \\ y &\le x-1 \end{aligned}$$
https://www.desmos.com/calculator/tthbvj4pdw
Die Lösungsmenge ist die Halbebene unterhalb der Geraden \(y=x-1\). Und die Gerade selbst ist Teil der Lösung.
zu 3.) \(\frac{|z+1|}{|z-1|}<1 \) da kann man schreiben$$\left|\frac{z+1}{z-1}\right| = \frac{|z+1|}{|z-1|} \lt 1 \quad \mathbb D = \{z \in \mathbb C \backslash 1\} \\ \implies |z+1| \lt |z-1|$$Bevor ich das ausrechne schaue Dir mal folgendes Bild an.
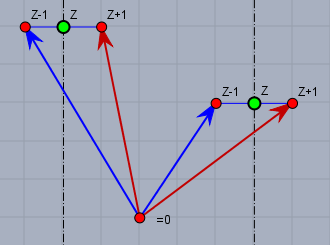
Ich habe zwei Beispiele für einen Punkt \(z\) (grün) in die Gauß'sche Zahlenebene gezeichnet. Sowie die Punkte \(z+1\) und \(z-1\). Die Absolutfunktion \(|z \pm 1|\) liefert als Ergebnis immer die Länge der blau und rot markierten Strecken vom Ursprung \(0\) zum jeweiligen Punkt in der Zahlenebene.
Wenn sich \(z\) links von \(0\) befindet ist der rote Pfeil immer kleiner als der blaue Pfeil. Liegt \(z\) rechts von \(0\), ist es umgekehrt. Obige Ungleichung ist erfüllt, wenn \(|z+1|\lt|z-1|\) also wenn rot kürzer als blau ist. Daraus folgt, dass die Lösungsmenge alle Punkte \(z\) sind, die links der imaginären Achse liegen; bzw. $$\mathbb L = \{z \in \mathbb C|\, \text{Re}(z) \lt 0\}$$
https://www.desmos.com/calculator/xg1druxopr
$$\begin{aligned} \left| \frac{z+1}{z-1} \right| &\lt 1 \\ |z+1| &\lt |z-1| \\ \sqrt{(x+1)^2 + y^2} &\lt \sqrt{(x-1)^2 + y^2} \\(x+1)^2 + y^2 &\lt (x-1)^2 + y^2 &&|\, - y^2\\ x^2 +2x + 1 &\lt x^2 - 2x + 1 &&|\, -(x^2 + 1) \\ 2x &< -2x &&|\, + 2x\\ 4x &\lt 0 &&|\, \div 4\\ x &\lt 0 \\ \implies \text{Re}(z) &\lt 0\end{aligned}$$
Gruß Werner
