Teilmenge von R2 auf Eigenschaften überprüfen 0<= y <= 1-x4

Question

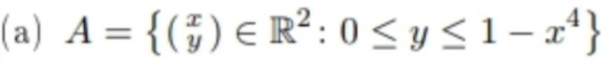
Text erkannt:

(a) $\left.A=\left\{\begin{array}{l}x \\ y\end{array}\right) \in \mathbb{R}^{2}: 0 \leq y \leq 1-x^{4}\right\}$

Aufgabe:

Untersuche die Teilmengen von R2  auf Kompaktheit Abgeschlossenheit Beschränktheit und Offenheit.

Problem/Ansatz:

Zur Verständnis: Soll x über y eine Matrix sein oder der Binomialkoeffizient? Oder eine alternative Darstellung für (x,y)?

Die Norm ist durch 0<= nach unten beschränkt , kann man die gesamte Teilmenge dann beschränkt nennen?

Im Komplement sind alle Zahlen z > 0 und z >= 1 ( Dann wäre die Teilmenge nach oben und unten beschränkt) ,richtig?

Wie kann ich hier die Offenheit bestimmen?

Answer 1

Zerlege $A=A_1\cap A_2$,so dass:$$A=\left \{\begin{pmatrix} x\\y \end{pmatrix}\in \mathbb{R}^2 : 0\leq y \leq 1-x^2\right\}=\underbrace{\left \{\begin{pmatrix} x\\y \end{pmatrix}\in \mathbb{R}^2 : 0\leq y \right\}}_{A_1}\cap \underbrace{\left \{\begin{pmatrix} x\\y \end{pmatrix}\in \mathbb{R}^2 : y\leq 1-x^2\right\}}_{A_2}$$ Betrachte nun $A_1$ und $A_2$ separat. Ich mache das für $A_2$.

Setze $f: \mathbb{R}^2\to \mathbb{R}, \, (x,y)\mapsto x^2+y-1$. Diese Funktion ist stetig. Dann ist $A_2^C=f^{-1}(\{z\in \mathbb{R} : z>0\})$, wobei $\{z\in \mathbb{R} : z>0\}$ offen in $\mathbb{R}$ ist. Damit ist $A_2^C$ das offene Urbild der Menge $\{z\in \mathbb{R} : z>0\}$ unter der stetigen Funktion $f$ und damit seinerseits offen in $\mathbb{R}^2$. Weil$A_2^C$ offen ist, ist $A_2$ abgeschlossen. Wenn du die Abgeschlossenheit von $A_1$ nachgewiesen hast, so ist der Durchschnitt ebenfalls abgeschlossen.

Merke: Urbilder offener/abgeschlossener Mengen unter stetigen Funktionen sind offen/abgeschlossen.