Wie viel cm hängt das seil in der mitte durch?

Question

Aufgabe: in der Mitte zwischen zwei gegenüberliegenden Masten einer Straße ist eine Straßenlaterne befestigt. Der abstand

der Masten beträgt 12m. Das seil ist 12,10 m lang.

Wie viel cm hängt das seil in der mitte durch?

Problem/Ansatz: könnte jemand anderes das zum abgleichen mal rechnen?

Comments

jemand anderes das zum abgleichen mal rechnen

Was ist denn dein Ergebnis, das du abgleichen möchtest?

---

also ich habe 10 cm weil es sind ja 10 cm zu viel seil

---

Vom Duplikat:

Titel: ich brauche immer noch hilfe, wie rechne ich das bloß?

Stichworte: funktion

Aufgabe:in der Mitte zwischen zwei gegenüberliegenden Masten einer Straße ist eine Straßenlaterne befestigt. Der abstand

der Masten beträgt 12m. Das seil ist 12,10 m lang.

Wie viel cm hängt das seil in der mitte durch?

Problem/Ansatz:

ich verstehe es immer noch nicht ich rechne das glaub ich irgendwie falsch das habe ich bis jetzt

https://www.mathelounge.de/?qa=blob&qa_blobid=14669744993182932565

---

Aufgabe:in der Mitte zwischen zwei gegenüberliegenden Masten einer Straße ist eine Straßenlaterne befestigt. Der abstand

der Masten beträgt 12m. Das seil ist 12,10 m lang.

Wie viel cm hängt das seil in der mitte durch?


Problem/Ansatz:

ich verstehe es immer noch nicht ich rechne das glaub ich irgendwie falsch das habe ich bis jetzt



https://www.mathelounge.de/?qa=blob&qa_blobid=14669744993182932565

---

Auf deiner Skizze steht 6 cm anstatt 6 m. Zudem muss die Wurzel über den ganzen Term gehen, nicht nur über den ersten Summanden.

---

ja hast recht   haha

---

Auch solltest du ein rechtwinkliges Dreieck zeichnen, wenn man dir etwas von Pythagoras erzählt. Dem sein Satz geht nur für rechwinklige Dreiecke. Das Dreieck auf deiner Skizze ist nicht rechtwinklig.

Answer 1

Ich denke 10cm, weil es ja 10cm zu viel Seil ist.

Answer 2

Ich komme auf ca. 78 cm. Pythagoras !

Zeichne dir ein Dreieck:

halber Mastenabstand ( 6m)

Das schräg nach unten verlaufende Seil ( 6,05m)

und die dritte Seite ist der "Durchhang"

siehe auch https://www.mathelounge.de/820092/wie-viel-hangt-das-seil-in-der-mitte-durch

Comments

Das Seil bildet doch eine Parabel.

Wie kann man bei einer Krümmung mit dem Pythagoras arbeiten?

Ich kann mir das gerade nicht vorstellen.

Ist nicht der Scheitel der Parabel gesucht oder mache ich einen Denkfehler?

---

Das Seil bildet doch eine Parabel.

Wenn eine Lampe dran hängt, dann nicht.

Wenn keine Lampe dran hängt, dann eine Kettenlinie. Joachim Jungius wies im 17. Jahrhundert nach, dass die Kettenlinie keine Parabel ist.

In jenem Fall müsste man das Gleichungssystem

a cosh(\( \frac{6}{a} \)) + c = 0

2a sinh(\( \frac{12}{2a} \)) = 12,1

lösen, käme auf

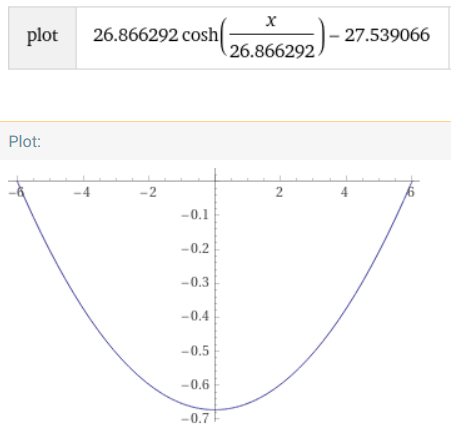
und einen Durchhänger von etwa 67,3 cm.

---

Danke für den Hinweis.

Doch wenn ich das bei wiki nachlese, bin ich so schlau wie zuvor.

https://de.wikipedia.org/wiki/Kettenlinie_(Mathematik)

Der Sachverhalt erscheint mir so komplex.

---

danke sehr aber kannst du bitte noch mal ganz genau erklären wie man das rechnet?

---

Das schräg nach unten verlaufende Seil (6,05 m) vom Mast zur Lampe ist die Hypotenuse, also das c im Satz von Pythagoras, und die 6 m lange horizontale Kathete auf Deiner Zeichnung ist b. Aus a² + b² = c² folgt a = \( \sqrt{c^2-b^2} \).

Meine Ausführungen für den Fall ohne Lampe und das dann bogenförmig hängende Seil bezogen sich auf die Bemerkung eines anderen Benutzers. Du kannst sie getrost ignorieren. Im Fall mit Lampe verläuft das Seil geradlinig, weil es ja von der Lampe gespannt wird.

---

alles klar danke sehr ich habe es jetzt verstanden