Wie bestimme ich f(x)=x², g(x)= 1,5x+1 zeichnerisch?

Question

Aufgabe:

Die gemeinsamen Punkte von f(x)=x², g(x)= 1,5x+1 zeichnerisch bestimmen. Und dann rechnerisch überprüfen

Problem/Ansatz:

Ich habe eine Aufgabe erhalten in welcher ich f(x)=x², g(x)= 1,5x+1 zeichnerisch bestimmen und dann rechnerisch überprüfen soll. Ich verstehe wie letzteres geht, jedoch weiß ich nicht wie man so etwas zeichnerisch bestimmt.

Comments

Zeichne die Funktionsgraphen der beiden Funktionen.

---

Hallo,

man kann diese Aufgabe auch zeichnerisch (besser konstruktiv) ohne Wertetabelle lösen. Dazu ist die Kenntnis notwendig, dass eine Parabel über ihren Brennpunkt $F$ und eine Leitlinie definiert sein kann. Die Idee hinter der Konstruktion ist, dass auch die Tangenten an die Parabel in den Schnittpunkten der Parabel $x^2$ mit der Geraden $1,5x+1$ diese in den gleichen Punkten schneiden.

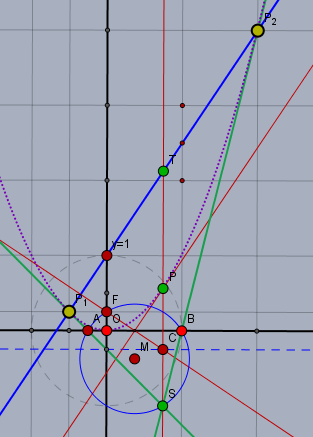
Zeichne dafür eine Koordinatensystem mit dem Brennpunkt $F$ bei $F(0|\,0,25)$ und der Leitlinie bzw. Leitgeraden $l$ bei $y=-0,25$ (blau gestrichelt). Den Graphen der Funktion $y=1,5x+1$ als Gerade $g$ (blau) dort einzuzeichnen sollte kein Probem sein.

Nun folgt die Orthogonale zu $g$ (rot) durch $F$, die $l$ in $C$ schneidet. Die Mittelsenkrechte zu $FC$ (rot) schneidet die Orthogonale zu $l$ durch $C$ (rot) im Punkt $P$. $P$ ist bereits ein Punkt der Parabel und die Mittelsenkrechte ist die Tangente zur Parabel in $P$. Die Orthogonale (rot) zu $l$ durch $C$ bzw. $P$ schneidet $g$ im Punkt $T$ (grün).

Spiegelt man $T$ an $P$ kommt man zum Punkt $S$ (grün), der der Schnittpunkt der beiden gesuchten Tangenten ist. $M$ ist der Mittelpunkt der Streck $FS$. Der Kreis (blau) um $M$ mit Durchmeser $|FS|$ schneidet die Tangente im Scheitel der Parabel - d.h. hier die X-Achse (schwarz) - in den Punkten $A$ und $B$. Die Geraden durch $AS$ bzw. $BS$ (grün) sind die gesuchten Tangenten, die $g$ in $P_1$ und $P_2$ (gelb) schneiden.

Konstruiert man sich noch ein Gitternetz im Koordinatensysem, so kann man die Koordinaten von $P_{1,2}$ ablesen$$P_1\left( -\frac 12\mid\, \frac 14\right), \quad P_2(2|\,4)$$

Answer 1

Zeichne die Parabel y=x² in ein Koordinatensystem. (Benutze notfalls eine Wertetabelle).

Zeichne auch die Gerade y=1,5x+1 in das gleiche Koordinatensystem (die Kenntnis von Anstieg und Schnittpunkt mit der y-Achse macht eine Wertetabelle eigentlich überfüssig, aber wenn meine Erwartungshaltung zu hoch ist, dann mache lieber auch hier eine).