Ich hätte eine Frage zur Berechnung der FT.
Aufgabe:
Berechnen Sie die Fouriertransformierte.
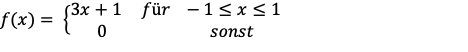
Text erkannt:
\( f(x)=\left\{\begin{array}{ccc}3 x+1 & \text { für } & -1 \leq x \leq 1 \\ 0 & \text { sonst }\end{array}\right. \)
Problem/Ansatz:
Mein Ansatz:
Erst das Integral zu zerlegen (f1(x) und f2(x)) und die Stammfunktionen bilden. Danach addieren und lösen, dabei sollte eigentlich kein Fehler passiert sein. Meine Frage basiert eher auf dem letzten Teil wo ich zusammenfasse und in sin-cos-Terme umforme. Darf man das so machen? Ich berufe mich dabei auf den Zusammenhang
r·e-ix = r·(cos(x)-sin(x))
r·eix = r·(cos(x)+sin(x)).
:)

Text erkannt:
\( =\int \limits_{-1}^{1}(3 x+1) e^{-l \omega x} d x=\int \limits_{-1}^{1} 3 x e^{-t \omega x} d x+\int \limits_{-1}^{1} e^{-t \omega x} d x \)
Stammfunktionen berechnen und zusammenfassen
\( F_{1}(x)=\left[\frac{3 k x}{\omega} e^{-(\omega x]}\right]_{-1}^{1}-\int \limits_{-1}^{1} \frac{3 t}{\omega} e^{-\operatorname{tax}} d x=\left[\frac{3 x t}{\omega} e^{-\operatorname{lox} x}+\right. \)
\( \left.\frac{3}{\omega^{2}} e^{-t \omega x}\right]_{-1}^{1} \)
\( F_{2}(x)=\left[\frac{t}{\omega} e^{-\operatorname{lox} x}\right]_{-1}^{1} \)
\( F_{1}(x)+F_{2}(x)=\left[\frac{3 x d}{\omega} e^{-(\omega x)}+\frac{3}{\omega^{2}} e^{-l \omega x}+\frac{i}{\omega} e^{-\operatorname{lov} x}\right]_{-1}^{1} \)
Integral berechnen
\( =\frac{3 t}{\omega} e^{-t \omega}+\frac{3}{\omega^{2}} e^{-t \omega}+\frac{l}{\omega} e^{-l \omega}+\frac{3 t}{\omega} e^{l \omega}-\frac{3}{\omega^{2}} e^{t \omega}-\frac{l}{\omega} e^{l \omega} \)
\( =\left(\frac{3 t}{\omega}+\frac{3}{\omega^{2}}+\frac{t}{\omega}\right) e^{t \omega}+\left(\frac{3 t}{6}-\frac{3}{\omega^{2}}-\frac{4}{\omega}\right) e^{-\mathrm{ta}} \)
\( =\left(\frac{3 t \omega+3+l \omega}{\omega^{2}}\right) e^{t \omega}+\left(\frac{3 t \omega-3-l \omega}{\omega^{2}}\right) e^{-i \omega} \)
Mit der Euler'schen Formel in trigonometrische Form umwandeln

Text erkannt:
\( =\frac{3 t \omega+3+\operatorname{lo}}{\omega^{2}}(\cos (\omega)+i \sin (\omega))+\frac{3 i \omega-3-L \omega}{\omega^{2}}(\cos (-\omega)- \)
\( i \sin (-\omega)) \)
$$ \overline{f(\omega)=\frac{3 i \omega+3+i \omega}{w^{2}}(\cos (\omega)+i \sin (\omega))+\frac{3 i \omega-3-i \omega}{w^{2}}(\cos (-\omega)-i \sin (-\omega))} $$
Text erkannt:
\( F_{1}(x)=\left[\frac{a_{w}}{*}-k+1_{-1}^{1}-\int \limits_{-1}^{1}\right. \)
\( F_{2}(x)=\left[\frac{1}{x}--\operatorname{lan} 1\right]_{-1}^{1} \)
\( \widehat{f(\omega)}=\frac{3 i \omega+3+i \omega}{w^{2}}(\cos (\omega)+i \sin (\omega))+\frac{3 i \omega-3-i \omega}{w^{2}}(\cos (-\omega)-i \sin (-\omega)) \)
Text erkannt:
\( -\left(\frac{4}{w}+\frac{7}{w}+\frac{1}{4}\right) \cdot t^{\omega}+\left(\frac{4}{w}-\frac{3}{x}-\frac{1}{4}\right) a^{-\infty} \)
\( \widehat{f(\omega)}=\frac{3 i \omega+3+i \omega}{w^{2}}(\cos (\omega)+i \sin (\omega))+\frac{3 i \omega-3-i \omega}{w^{2}}(\cos (-\omega)-i \sin (-\omega)) \)