
Ich weiß zwar nicht, ob sich hier jemand findet, der das liest, aber bekanntlich hat ja jede Erörterung ihren Adressaten.
Ob die Überschrift so glücklich gewählt ist, sei einmal dahingestellt.
Mir geht es um zweigliedrige Produkte, in welchen Differenzen auftreten, also (a+b)(c-d), (a-b)(c-d) und die speziellen Fälle (a+b)(a-b), (a-b)(a-b). Ausgehen läßt sich dabei vom allg. Distributivgesetz a(b-c). Dafür findet sich z.B. bei Kusch 1(15.Aufl.) S.72 die soweit bekannte Regel: Man multipliziert eine Summe oder Differenz mit einer Zahl oder Variablen, indem … und die erhaltenen Produkte addiert oder subtrahiert, je nachdem, welches Rechenzeichen vor dem jeweiligen Glied in der Klammer steht. Auf der folgenden Seite wird dieselbe Regel nochmals allg. für Summen formuliert, verbunden mit dem Hinweis auf die bekannten Vorzeichenregeln. Für den Fall (a-b)c
gibt es auch ein entsprechendes Diagramm, welches dem auf dieser Seite entspricht:
http://www.mathematische-basteleien.de/formel.htm
Ein solches Produkt wird bei Kusch 1 S. 71 übrigens so erklärt: n(a-b) bedeutet, a und -b als Summanden n-mal zu setzen. Nun frage ich mich, ob ich ein Produkt wie -b•c überhaupt geometrisch interpretieren kann. Denn das Rechenzeichen in der Klammer wird doch beim Ausmultiplizieren zum Vorzeichen - oder? Nun sind allerdings geometrische Größen stets positiv, weshalb ja auch in Fällen wie (a-b)(c-d) a stets größer als b bzw. c > d sein muß - jedenfalls wenn ich es geometrisch deuten will. Aber auch die Subtrahenden sind ja eigentlich nicht negativ.
Interpretiere ich ein Produkt zweier Größen/Zahlen als Rechteck so habe ich eine Fläche bzw. einen Flächeninhalt und der ist immer größer 0 und die beiden Größen sind auch positiv. Nun wird in der genannten Regel auf das Rechenzeichen verwiesen, ohne daß dabei klar ist, welches jeweilige Glied gemeint ist. Wenn ich in einem Produkt wie (x+3)(4-x) 3 mit x multipliziere, habe ich ja zwei Rechenzeichen und bei x•4 gar keins.
In Algebra 1(Fr. Barth 1.Aufl.) wird S.65 definiert: 1. Für das Produkt aus einer positiven Zahl p und einer negativen Zahl -q soll gelten: p•(-q) = -(p•q). 2. Für das Produkt aus einer negativen Zahl -p und einer positiven Zahl q soll gelten: (-p)• q = -(p•q). Beides wird zu der Regel zusammengefaßt, daß man das Produkt aus einer positiven und einer negativen Zahl erhält, indem man das Minuszeichen des negativen Faktors vor das Produkt der beiden Beträge setzt, also das Minuszeichen(=negative Vorzeichen?) „herauszieht“, wie es dort auch heißt. Gleichwohl heißt es auf derselben Seite, daß die Variablen p und q positive Zahlen vertreten. Aber wenn z.B. -q eine negative Zahl sein soll, wie kann sie dann eine positive vertreten? Beim Produkt zwei negativer Zahlen sollen dann nur noch die Beträge multipliziert werden. Auf S. 75ff.(2.6.4 Allgemeine Vorzeichenregeln für Produkte und Quotienten) wird das wieder aufgegriffen und auf beliebige rationale Zahlen erweitert und die bekannten Vorzeichenregeln allg. aufgeführt. So jedenfalls werden sie ja immer bezeichnet. Nun kann ich ja auch schreiben (5+2)(5-(+2)), (5-(+2))(5-(+2)), denn sowas wie (5+(-2)) schließt sich ja aus. Schließlich will ich das geometrisch deuten bzw. beweisen. Aber spätestens beim Multiplizieren der Subtrahenden haben ich wieder zwei Rechenzeichen.
Nun gibt es schon bei Diophant eine vergleichbare Regel, wonach - • + = - und - • - = + ist, wenn man es denn so wiedergibt, d.h. die im folgenden genannten Begriffe. Dabei möchte ich betonen, daß es mir nicht um die Frage geht, ob Diophant negative Größen/Zahlen kannte bzw. anerkannte.
Ich benutze das nur als „Aufhänger” für meine grundsätzliche Fragestellung.
Dabei beschäftigen mich die geometrischen Deutungsversuche eines Scholiasten aus dem 13.Jhd., Maximos Planudis(Planudes) genannt. Ob er Diophant gerecht wird oder nicht, ist für mich auch nicht entscheidend. Nach ihm ist in dem Term 6-x die 6 ὕπαρξις und das x λείψις. Also etwa Minuend und Subtrahend. Er betont dabei nämlich, daß das „Fehlen“(λείψις) nur zusammen mit etwas „Bestehendem”(ὕπαρξις) zu denken sei.
Nun kann man m.E. nicht per se davon ausgehen, daß Maximos Planudis keine negativen Zahlen kannte. Immerhin war ihm die indische Mathematik nicht unbekannt.
Um nun (5-x)(5-x) geometrisch zu beweisen, nimmt er ein Quadrat unterteilt in Einheitsquadrate.
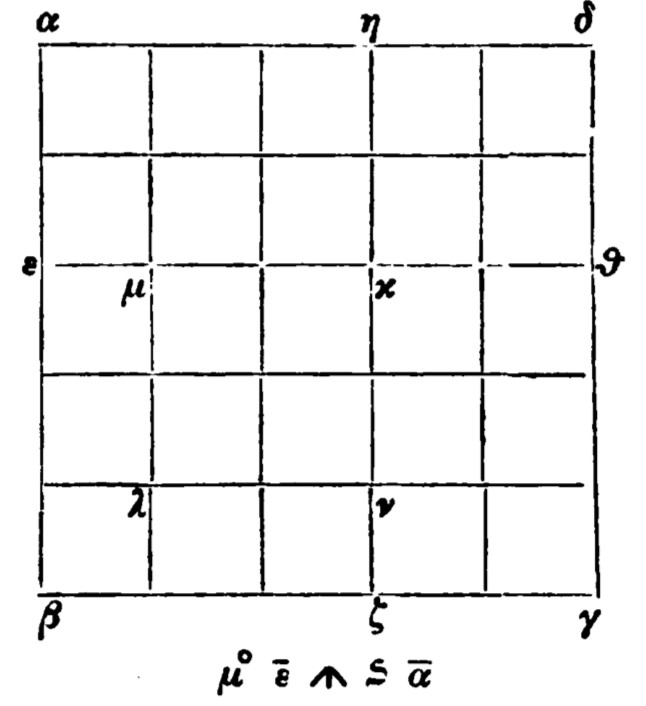
Das Bild habe ich direkt aus dem griechischen Text. Das griechische Alphabet sollte den Profis hier soweit geläufig sein. Das unter dem Diagramm bedeutet 5-x. Der Text selbst ist recht umständlich, durchaus nicht leicht verständlich und irgendwie auch redundant. Ich mache es möglichst kurz.
αε und ζγ sind dabei jeweils die Subtrahenden. Zu Beginn freilich beweist er nichts, sondern setzt für x einfach 2 ein, berechnet die Differenz und quadriert sie.
Erst darnach fängt er an, dies auch geometrisch zu verifizieren. Also (αβ-αε) (βγ-ζγ).Dabei geht er ganz so wie heute vor. Erst αβ•βγ, also 5•5, dann αβ•ζγ = ζγδη, αε•βγ = εθδα. Beides zieht er ab, stellt aber fest, daß κθδη damit zweimal abgezogen wäre. Das aber sei unmöglich(und ist es auch), also nimmt er dann das dem κθδη gleiche Quadrat λνκμ und als Rest bleibt dann der Gnomon βζνλμε. Da nun die λείψεις αε, ζγ bzw. wohl eher deren Produkte abgezogen seien, blieben noch jeweils εβ, βζ = 3, quadriert gleich 9. Da aber der Gnomon nur 5 sei, müsse man ihm wieder 4 hinzuaddieren, um auf 9 zu kommen und das Quadrat zu vervollständigen. Und dies sei eben -x • -x= x^{2}. Gleichzeitig betont er, daß man dies eben auch herausbekommen hätte, wenn man einfach die Differenzen - wie am Anfang - multipliziert hätte. So aber ergebe sich x^{2}+25-10x. Dafür gibt er dann eine Übersicht:
5 - x
5 - x
-
25 5x
x^{2} 5x
———————
25+x^{2}- 10x
Das entspricht zwar nicht seiner Beweiskette, ist aber recht einfach verständlich. Steht in einem Faktor ein Pluszeichen ist das weniger einsichtig. Aber das lasse ich hier mal weg. Für meine grundsätzliche Frage reicht das Dargestellte.
Sogesehen ergäbe dann Minuend mal Minuend bzw. Subtrahend mal Subtrahend jeweils einen Summanden und Minuend mal Subtrahend bzw. Subtrahend mal Minuend jeweils einen Subtrahenden. Immerhin muß ich bei einer geometrischen Interpretation ohnehin die Summanden zuerst nehmen. Insofern ist das abschließende Schema des Scholiasten richtiger als sein Beweis.
Denn sobald in dem besprochenen Fall, wenn ich jetzt mal von (a-b)(a-b) ausgehe, b =$$ \frac{1}{2} $$a
od. > $$\frac{1}{2}$$a ist, lande ich bei Null bzw. werde negativ. Und auch der geometrische Beweis des Herrn Planudis funktioniert dann in der Form nicht mehr.
Dementsprechend wird das auf der eingangs zitierten Webseite auch gemacht. Bei einem Rechteck mit Gnomonfigur bin ich bei normaler Reihenfolge beim 3. Schritt immer bei Null.
Auf den Scholiasten geht übrigens schon Otto Schulz in seiner dt. Diophantausgabe ein.
https://www.e-rara.ch/zut/content/titleinfo/16066831
So meint er im Vorbericht S. XXIX, daß er z.B. +5 mit -x multiplizieren wolle. Dieses Minuszeichen bei x kann ich aber doch nur als Vorzeichen auffassen? Nur wie soll ich +5 • -x als Rechteck deuten?
In seinen Anmerkungen S. 344 ff. führt er das von mir Geschilderte auch an, dreht allerdings bei den Mittelgliedern gegen den Text die Reihenfolge um. Das möchte er dann noch mit einem beliebigen Zahlenbeispiel erläutern und nimmt (9-4)(7-3). Er rechnet dann (9-4)7 - 3(9-4). Das entspricht zwar nicht dem Scholion, interessant ist aber, daß er meint, daß sich daraus die Regel für die Vorzeichen eines Produktes befriedigend herleiten lassen, wenn man gleich negative Größe
in dem eingeschränkten arithmetischen Sinne nehme. Was er mit letzterem meint, geht es aus dem Beginn seiner Ausführungen S.344 hervor. Darnach nenne Diophant eine negative Zahl λείψις, d.h. eine fehlende Größe oder eine, welche man subtrahieren solle, eine positive Zahl aber
ὕπαρξις, d.h. eine wirklich vorhandene, die einem wirklich bestimmten Wert habe. Mich irritiert daran, die de facto Gleichsetzung eines Subtrahenden mit einer negativen Zahl/Größe. Ich mein, wenn mich bei einem Term wie 3-5 jemand fragte, wo dort eine negative Zahl sei, dann wäre das doch der ganze Ausdruck, also -2? Und bei 5-3 gäbe es gar keine - oder? Und bei den mehrgliedrigen Produkten komme ich da um so mehr ins Schlingern. Immer unter der Voraussetzung natürlich, daß ich „Flächenalgebra“ betreibe.
Der Vollständigkeit halber sei erwähnt, daß sich der Mathematiker Klaus Barner ausführlich mit negativen Größen bei Diophant beschäftigt hat.
Der 1. Teil ist online
https://kobra.uni-kassel.de/handle/123456789/200604048979 und ich kenne auch nur den. Den 2. kann man bei Springer für relativ viel Geld kaufen.
Momentan fehlt mir aber die Zeit, mich damit und mit Diophant weiter zu befassen. Zudem bin ich kein studierter Mathematiker und brauche dann immer etwas länger. Aber wenn ich Herrn Barner richtig verstehe, der zahlreiche Fundstellen bei Diophant analysiert, dann ist λείψις bei Diophant eine negative Differenz.
Meine grundsätzliche Frage sollte klar sein. Habe ich Produkte mit Differenzen und stelle ich die geometrisch dar bzw. beweise sie geometrisch, ist es dann nicht richtiger bzw. zwingend mit den natürlich positiven Differenzen zu arbeiten und auf das Ausmultiplizieren zu verzichten, weil ich dann Produkte mit negativen Größen habe? Und zeigt sich das nicht an den Deutungsversuchen des Scholiasten.