Ich denke das läuft auf dasselbe hinaus. Ich arbeite jetzt mal mit dem Königsberger Band II und dem dortigen Satz zur lokalen Nullstellenmenge (in der 5. Auflage Seite 117)
Wenn \( b \in \mathbb R \) und \( (x_0, y_0) \in f^{-1}(b) \) beliebig. Dann wählen wir als Umgebung erstmal \( \mathbb R^2 \) und es ist
$$ f^{-1}(b) \cap \mathbb R^2 = \{ (x,y) \in \mathbb R^2 ~|~ f(x,y) = b \} = \{ (x,y) \in \mathbb R^2 ~|~ f(x,y) -b = 0 \} $$
Die Funktion \( F : \mathbb R^2 \to \mathbb R, (x,y) \mapsto f(x,y) - b \) ist sicherlich eine \( C^1 \)-Funktion.
Fehlt noch dass das Differential \( dF_{(x_0,y_0)} \) linear unabhängig bzw. da nur eine Funktion vorliegt also ungleich 0 ist. Jetzt ist
$$ dF_{(x_0,y_0)} : \mathbb R^2 \to \mathbb R, x \mapsto \nabla F(x_0,y_0)^T \cdot x $$
Das ist nicht 0 falls der Gradient nicht 0 ist.
$$ \nabla F(x_0,y_0) = \begin{pmatrix} 3x_0^2 -3a \\ -2y_0 \end{pmatrix} \neq 0 \iff y_0 \neq 0 \lor x_0 \neq \pm \sqrt a $$
Falls \( a < 0 \) ist zweitere Bedingung immer erfüllt, da \( x_0 \) keine komplexe Zahl sein kann und somit immer \( x_0 \neq \pm \sqrt a \) gilt. Also hier hast du immer eine UMFK vorliegen.
Falls \( a \ge 0 \) kann aber evtl \( y_0 = 0 \) und \( x_0 = \pm \sqrt a \) gelten.
In diesem Fall müsste ja aber auch \( b = x_0^3 - 3ax_0 -y_0^2 \) sein, also \( b = \pm 2a \sqrt a \).
Falls \( a \ge 0 \) und \( b \neq \pm 2a \sqrt a \) ist das also auch eine UMFK.
Bleibt \( a \ge 0 \) und \( b = \pm 2a \sqrt a \) separat zu prüfen. Dazu einfach mal ein paar Bildchen zeichnen lassen (z.B. mit GeoGebra):
\( a = 0, b = 0 \):
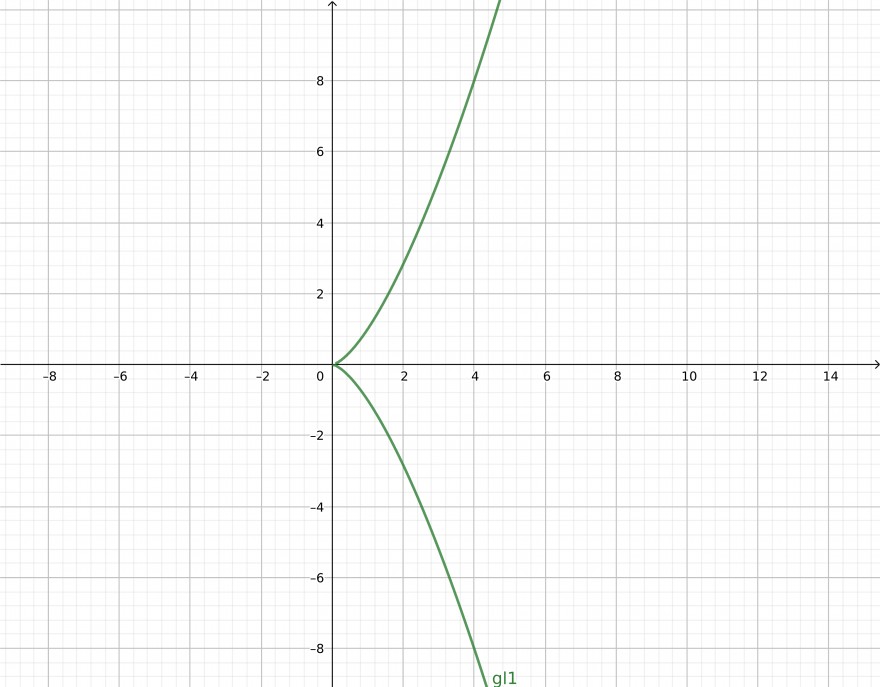
\( a > 0, b = +2a \sqrt a \)
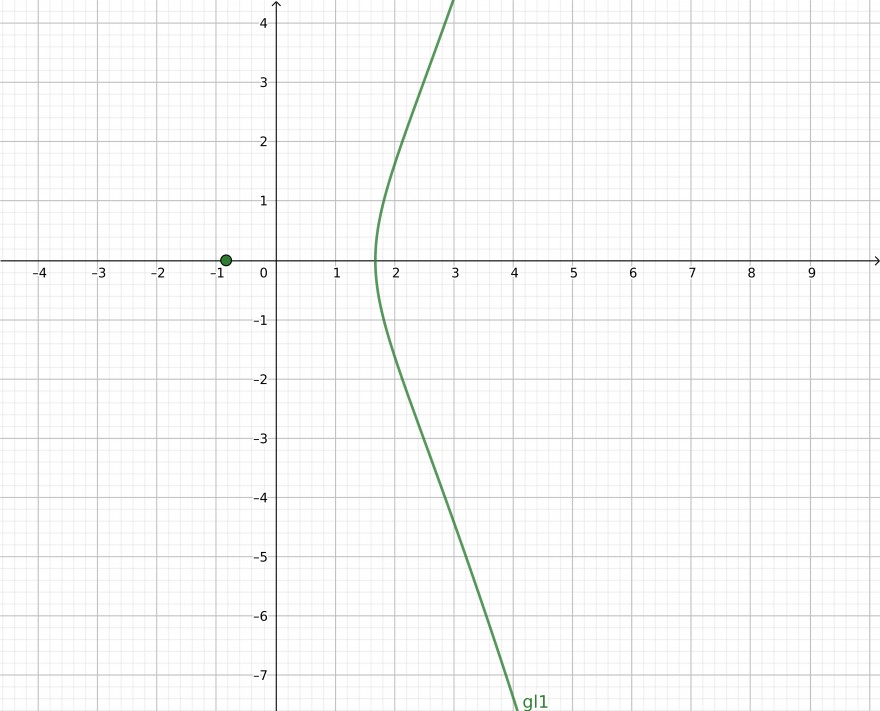
Hier aber den isolierten Punkt nicht vergessen!
\( a > 0, b = - 2a \sqrt a \)
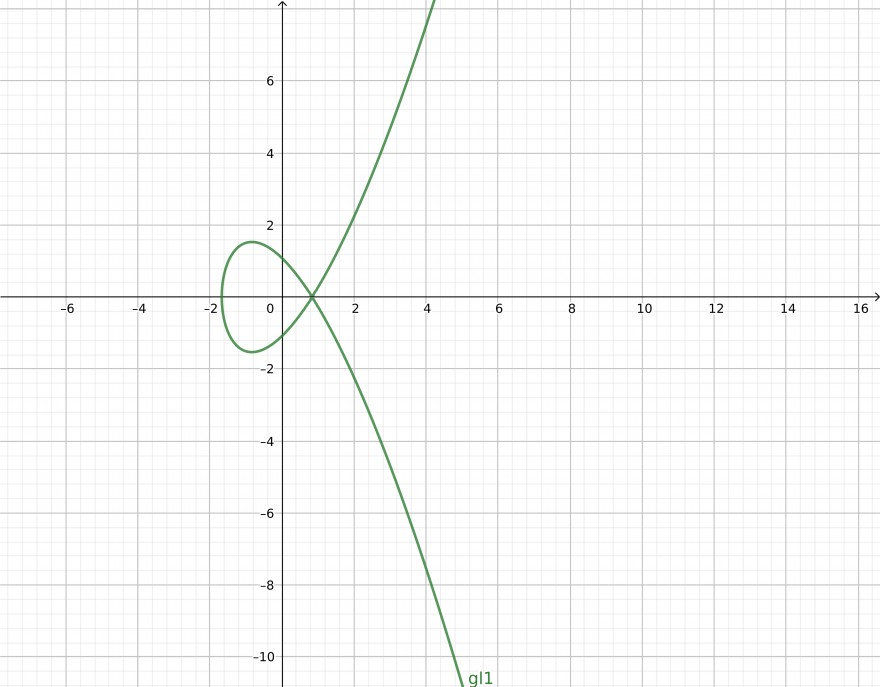 Würdest du sagen, dass das UMFK sind oder nicht?
Würdest du sagen, dass das UMFK sind oder nicht?