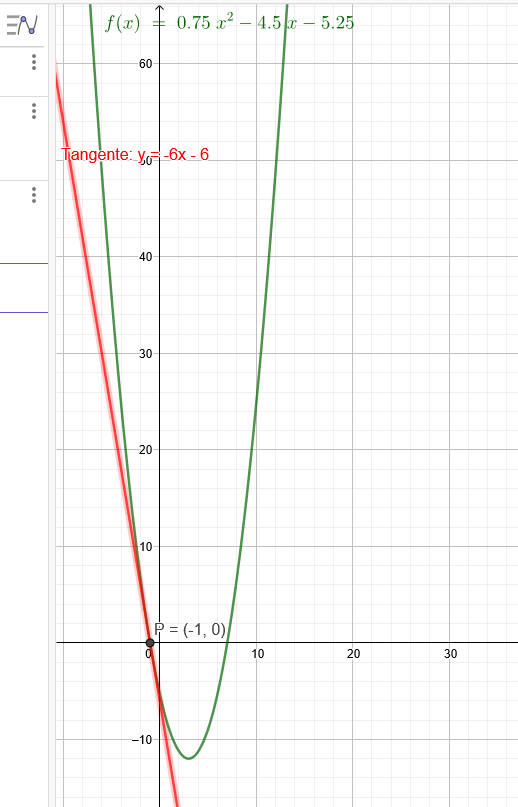
Der Graph der Funktion f (x) = 3x^2/4 + bx + c geht durch den Punkt P = (-1|0). Die Steigung der Tangente in P beträgt k = -6. Wie lautet die Gleichung der Funktion?
P (-1|0)
f (-1) = \( \frac{3}{4} \)* (-1)^2+ b*(-1) + c =
1.)\( \frac{3}{4} \)-b + c=0
f ´(x) = \( \frac{3}{2} \)x + b
f ´(-1) = \( \frac{3}{2} \)*(-1) + b
2.) \( \frac{3}{2} \)*(-1) + b=-6 → -1,5+b=-6 → b=-4,5
0,75+4,5 + c=0 →c=-5,25
f(x)=0,75x^2-4,5x-5,25