dadurch, dass du \( s = \frac{1}{2}at^2 \) noch nicht problemlos umstellen kannst, gehe ich davon aus, dass dir der Begriff "Integrale" noch nicht viel sagt. Was auch nicht schlimm ist, weil es für diese Formel auch eine nahezu rein physikalische Herleitung gibt.
Dafür schauen wir uns folgenden Graphen mal genauer an: Vorab sei gesagt, dass wir eine gleichbleibende Beschleunigung betrachten. Die Beschleunigung wird über die Zeit also nicht verändert. Bringen wir nun Messgeräte am Auto an, die die Strecke pro Zeit misst, erhalten wir folgenden Graphen:
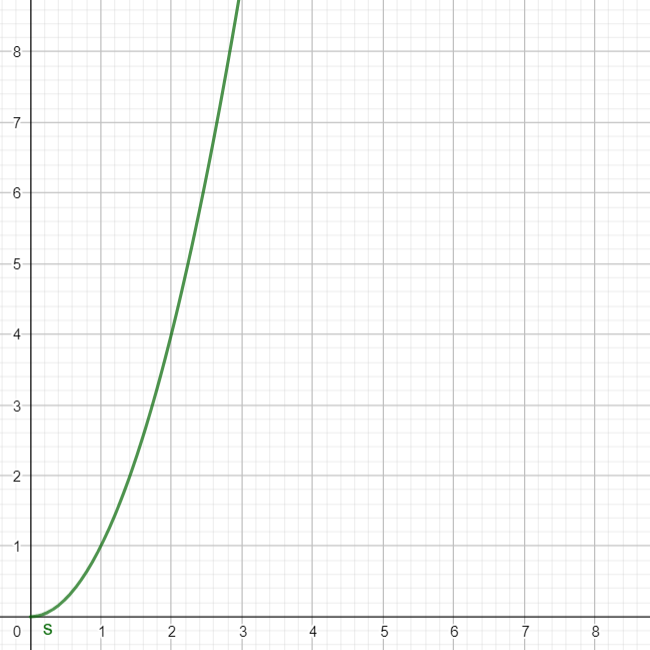
Unten ist die Zeit in Sekunden dargestellt und links die Strecke in Meter. Der grüne Graph stellt hier also die Strecke dar, die wir nach einer Zeit \( t \) erreichen werden oder erreicht haben. Nach 1 Sekunde sind wir 1 Meter weit gekommen. Nach 2 Sekunden sind wir in etwa 4 Meter weit gekommen. Nach 3 Sekunden sind wir etwa 9 Meter weit gekommen. Man kann sich so nun herleiten, dass wir zur Zeit \( t \) immer \( t^2 \) weit gekommen sind. Kontrolle:
- \(t = 1\) Sekunde \( \implies t^2 = 1^2 = 1 \) Meter.
- \(t = 2\) Sekunden \( \implies t^2 = 2^2 = 4 \) Meter.
- \(t = 3 \) Sekunden \( \implies t^2 = 3^2 = 9 \) Meter.
Man sagt hier also nun, dass die Strecke proportional zum Quadrat der Zeit ist:
\( s \sim t^2 \)
Wenn wir nun den Quotienten
\(\frac{s}{t^2}\)
berechnen, werden wir herausfinden, dass dieser immer konstant zu einer Zahl ist:
- 1 Sekunde, 1 Meter: \( \frac{1}{1^2} = \frac{1}{1} = 1 \)
- 2 Sekunden, 4 Meter: \( \frac{4}{2^2} = \frac{4}{4} = 1\)
- 3 Sekunden, 9 Meter: \( \frac{9}{3^2} = \frac{9}{9} = 1\)
Das kannst du nun beliebige lange so durchführen, du wirst immer eine \( 1 \) hier herausbekommen. Das gleiche kann man nun mit einer anderen Beschleingung machen, wobei hier dann eine andere Konstante herauskommen wird. Man hat dann herausgefunden, dass der Quotient \( \frac{s}{t^2} \) immer gleich einhalb mal der Beschleunigung ist:
\( \frac{s}{t^2} = \frac{1}{2}a \).
Multiplizieren wir diese Gleichung nun auf beiden Seiten mit \( t^2 \), erhalten wir:
\( s = \frac{1}{2}at^2 \).
Sollte noch etwas unklar sein, frag gerne nach.
Nun zu deiner Umformung nach der Beschleunigung:
Um Gleichungen nach einer Variablen, Zahl oder irgendeinem Symbol umstellen zu wollen, müssen wir sogenannte Gegenoperationen anwenden. Die Gegenoperation vom \( + \) ist das \( - \). Denn, haben wir die Zahl \( 5 \) gegeben und addieren \( 2 \) dazu, erhalten wir \( 5+2=7 \). Wollen wir nun unsere \( 5 \) zurück haben, subtrahieren wir mit \( 2 \), also \( 7 - 2 = 5 \). Die Gegenoperation vom \( \cdot \) ist das \( : \). Denn es gilt hier \( 5 \cdot 2 = 10 \) und \( 10:2 = 5 \). Es gibt noch viele weitere Gegenoperationen, auf die ich jetzt aber nicht weiter eingehen möchte, da die zwei oben genannten Gegenoperationen für diese Aufgabe ausreichen.
Also wagen wir uns mal an die Gleichung, die wir nach der Beschleunigung \(a\) umstellen wollen:
\( s = \frac{1}{2} \cdot a \cdot t^2 \)
Damit das \(a\) auf der rechten Seite alleine steht, müssen die \(\frac{1}{2}\) und das \(t^2\) weg. Wir bringen erstmal das \(t^2\) rüber. Dieses ist mit dem \(a\) mit dem Multiplikationszeichen verknüpft. Wir benötigen also die Gegenoperation von der Multiplikation, um das \(t^2\) wegzubekommen - wir teilen also auf beiden Seiten durch \(t^2\):
\(\frac{1}{t^2} \cdot s = \frac{1}{2} \cdot a \cdot t^2 \cdot \frac{1}{t^2}\).
Für Brüche gilt immer für jedes beliebiges \(x\): \(\frac{x}{x} = 1\). Also erhalten wir folglich:
\(\frac{1}{t^2} \cdot s = \frac{1}{2} \cdot a\).
Nun gilt es noch die \(\frac{1}{2}\) auf der rechten Seite wegzubekommen. Dabei sei erwähnt, dass \(\frac{1}{2} \cdot a\) das gleiche ist wie \( a:2 \). Wir benötigen also die Gegenoperation \( \cdot \), um die \(2\) wegzubekommen:
\( \frac{1}{t^2} \cdot s \cdot 2 = \frac{1}{2} \cdot a \cdot 2 \)
und damit
\( \frac{1}{t^2} \cdot s \cdot 2 = a \)
Schöner aufgeschrieben erhalten wir unsere gesuchte Gleichung:
\( a = \frac{2s}{t^2}\)
Sollte auch hier etwas unklar sein, frag nach.
Lg