Aufgabe:
Wir mussten folgenden Term ableiten.
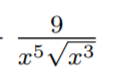
Text erkannt:
\( \frac{9}{x^{5} \sqrt{x^{3}}} \)
Mein Lösungsversuch:

Text erkannt:
ableiten:
\( \frac{9}{x^{5} \sqrt{x^{3}}} \)
1. Quotiontenragel
\( \frac{0 \cdot\left(x^{5} \sqrt{x^{3}}\right)-(5) \cdot\left(x^{5} \sqrt{x^{3}}\right)^{1}}{\left(x^{5} \sqrt{x^{3}}\right)^{2}} \)
\( \begin{array}{l} \left(x^{5} \sqrt{x^{3}}\right)^{\prime} \Rightarrow 2 \text { Produktrerd } \\ 5 x^{4} \cdot \sqrt{x^{3}}+x^{5} \cdot\left(\sqrt{x^{3}}\right)^{\prime} \\ \left(\sqrt{x^{3}}\right) \stackrel{1}{x} x^{\frac{3}{2}}=\frac{3}{2} \cdot x^{\frac{1}{2}} \Rightarrow \frac{3 \sqrt{7}}{2} \end{array} \)
3. einsetye
\( 5+4 \cdot \sqrt{x^{3}}+x^{5} \cdot \frac{3 \sqrt{x}}{2} \Rightarrow \frac{x^{5} \cdot 3 \sqrt{x}}{2}+5 x^{4} \sqrt{x^{3}} \) 4 wwitern mit \( -2 \)
\( \begin{aligned} \frac{x^{5} \cdot 3 r_{x}+10 x^{4} \sqrt{x^{2}}}{2} \\ \frac{-9\left(3 x \sqrt{x}+10 x^{4} \sqrt{x^{3}}\right)}{2\left(x^{5} \sqrt{x^{3}}\right)^{2}} \\ \Rightarrow \frac{-y x^{4}\left(3 x \sqrt{x}+10 \sqrt{x^{3}}\right)}{2 x^{13}} \\ \Rightarrow \frac{-\frac{9\left(3 x \sqrt{x}+10 \sqrt{x^{3}}\right)}{2 x^{y}}}{2} \end{aligned} \)
Was mache ich falsch? Ich habe es extra mit der Kettenregel versucht. Laut den Lösungen braucht man diese jedoch gar nicht. Warum muss man hier die Kettenregel nicht anwenden? Könnte man hier trotzdem die Kettenregel anwenden?
Vielen Dank im Voraus!