Question

Finden Sie das eindeutige Polynom f ∈ R[x] von Grad degf ≤ 3 mit
f(−2) = 0, f(0) = 1, f(1) = 0, f(4) = 0,st

Comments

Was willst Du mit dem "st" am Ende mitteilen?

Answer 1

Löse das System

0=-8a+4b-2c+1

0=a+b+c+1

0=64a+16b+4c+1

und setze die Lösungen in f(x)=ax³+bx²+cx+1 ein.

Answer 2

Da $-2,1,4$ die Nullstellen von $f$ sind, muss $f$ die Gestalt

$f(x)=a\cdot(x+2)(x-1)(x-4)$ haben und wir müssen nur noch $a$

bestimmen: $1=f(0)=a\cdot2\cdot (-1)\cdot (-4)=8a$, d.h. $a=\frac{1}{8}$.

Answer 3

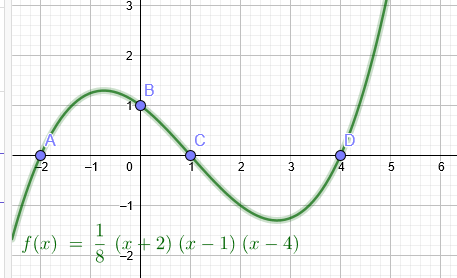
Finden Sie das eindeutige Polynom f ∈ R[x] von Grad degf ≤ 3 mit
f(−2) = 0, f(0) = 1, f(1) = 0, f(4) = 0

A(-2|0)   B(0|1)  C(1|0)   D(4|0)

Nullstellenform der kubischen Parabel:

f(x)=a*(x-(-2))(x-1)(x-4)=a*(x+2)(x-1)(x-4)

B(0|1)

f(0)=a*(0+2)(0-1)(0-4)=8a

8a=1    a=$\frac{1}{8}$

f(x)=$\frac{1}{8}$*(x+2)(x-1)(x-4)