Beweis des Satzes von Pythagoras: Warum ist da kein c²-2ab?

Question

Flächeninhalt gesamtes Quadrat $(a+b)^{2}$

Ein Dreieck hat die Fläche $a b / 2$

zieht man die Dreiecke ab, ergibt sich $\mathrm{c}^{2}$, also $(a+b)^{2}=c^{2}-4^{*} a b / 2$

umgestellt ergibt das $a^{2}+2 a b+b^{2}=c^{2}+2 a b$

abzüglich 2ab auf beiden Seiten $a^{2}+b^{2}=c^{2}$

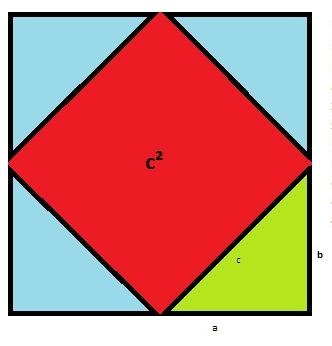
Warum ist da kein c²-2ab? Umgestellt von c²-4*ab/2.

Comments

Mehr zum Pythagoras auch: https://www.matheretter.de/wiki/pythagoras

und bei https://www.mathelounge.de/48029/mathe-artikel-der-satz-des-pythagor…

Answer 1

Wir setzten die beiden Quadrate gleich und insofern müsste es lauten

(a + b)^2 = c^2 + 4·1/2·a·b

Du kannst ja nicht noch etwas von c^2 wegnehmen um das große Quadrat zu erhalten.

Man könnte auch schreiben

c^2 = (a + b)^2 - 4·1/2·a·b

Answer 2

Hi,


Das Minus ist ein Fehler:


das ganze Quadrat ist also: (a+b)^2 = c^2 + 2ab !

Sonst wäre die Fläche ja kleiner als das gesamte Quadrat, was nicht sinnvoll wäre.