Wie ist der Funktionsterm für diese Aufgabe?

Question

Aufgabe:

Ich brauche einen Funktionsterm für diese Aufgabe

Problem/Ansatz:

Comments

Bereits das Gegebene ist falsch.

(-1|0), (0|0) und (2|0) sind keine Nullstellen der gegebenen Funktion.

---

wieso sie berühren ja die x-Achse.

---

wieso sie berühren ja die x-Achse.

Das wird ja noch schlimmer.

Erstens: "Sie berühren"

Wir haben nicht mehrere Funktionen, sondern nur die eine.

Zweitens: "Berühren" (der Achse) findet nur an der Stelle x=2 statt. Bei x=-1 und x=0 geht es um "Schneiden" der x-Achse.

Drittens (mein urprünglicher Kritikpunkt): Was du genannt hast sind keine Nullstellen, sonbdern gemeinsame Punkte von Graph und x-Achse. Nullstellen sind einfach nur Zahlen Die Nullstellen sind hier x=-1 und x=0 und (als doppelte Nullstelle) x=2.

---

Das ist alles unwichtig für mich.

Answer 1

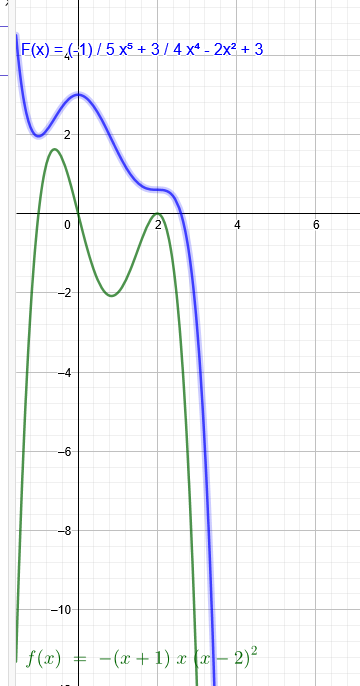
Der Graph von f(x) hat eine einfache Nullstelle bei N_1(-1|0) und bei N_2(0|0).

Bei N_3(2|0) existiert eine doppelte Nullstelle:

Polynom 4.Grades

f(x)=(x+1)*x*(x-2)²=x⁴-3x³+4x→

Überprüfung auf Richtigkeit:

f´(x)=4x³-9x²+4

f´(-1)=4*(-1)³-9*(-1)²+4=-9

Da der Graph von f(x) aber dort eine positive Steigung hat , gilt

f(x)=-(x+1)*x*(x-2)²=-x⁴+3x³-4x

F(x)=-$\frac{1}{5}$x^5+$\frac{3}{4}$x^4-2x^2+C

P(0|3)

F(0)=C→C=3

F(x)=-$\frac{1}{5}$x^5+$\frac{3}{4}$x^4-2x^2+3

Comments

Der Graph von f(x) hat eine einfache Nullstelle bei N_1(-1|0) und bei N_2(0|0).

Bei N_3(2|0) existiert eine doppelte Nullstelle:

Kannst du mal bitte dieses unkonkrete Geschwurbel lassen und konkrete Fachbegriffe verwenden?

Der Fragesteller (oder möglicherweise sogar die LEERkraft) geht mit dem Begriff "Nullstelle" schon fahrlässig um.

---

F(x)=-$\frac{1}{5}$x^5+$\frac{3}{4}$x^4-2x^2+3   stimmt nicht.

Richtig wäre F(x) = -1/21*(4x⁵-15x⁴+40x²-63)

Answer 2

Hallo

f hat 2 Extrma a und geht von -oo nach -oo also muss es eine Funktion 4 ten Grades sein. du kennst einige Werte, Nullstellen , Extrem stellen also in eine allgemeine Gleichung 4 ten Grades einsetzen

F ist zu schlampig gezeichnet: da F von +oo nach -oo geht ist der Grad ungerade, 3 oder 5. wenn die Stelle wo sich 2 Striche kreuzen eine Wendestelle ist, dann mindestens 5 ten Grades sonst  reicht dritten Grades

Gruß lul

Comments

also muss es eine Funktion 4 ten Grades sein.

Eine kühne Behauptung. Für f kennen wir nichts weiter als eine zittrige Freihandskizze. Solange nicht zweifelsfrei angegeben wurde, dass es sich um eine ganzrationale Funktion dritten Grades handel (und nicht um fünften Grad oder irgendwas abgefahrenes) ist das nur Kaffesatzleserei.

Answer 3

F ( 0) = 3
F ´( 0 ) = 0
F ( -1 ) = 0
F ´( 2 ) = 0
F ( -1 ) = 2

Stimmen die Punkte so ?

F ( x ) = a*x⁴ + b*x³ + c* x² + d*x + e
F ´( x ) = 4a*x³ + 3b * x² + 2cx + d

geht gleich weiter
Brunner meint allerdings das gäbe so nichts.