Hallo,
Die Lösung ist doch schon halb gegeben:
(Hinweis: Simson-Gerade)
Bei der Simsom Gerade liegt ein Punkt auf dem Umkreis vor und die Fußpunkte der Lote von diesem Punkt aus, auf die Seiten eines Dreiecks bzw. dessen Verlängerungen, liegen auf einer Geraden.
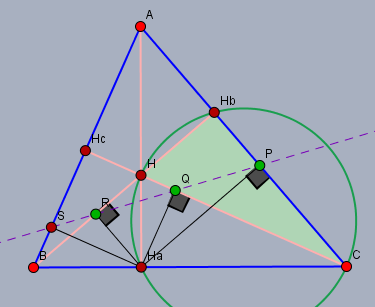
Der Punkt, von dem die meisten Lote ausgehen ist hier \(H_a\). Und drei der Lote gehen auf die Geraden \(BH_b\), \(HC\) und \(AC=b\). Und damit liegen bereits die drei Seiten des Dreiecks \(\triangle HCH_b\) fest.
Jetzt bleibt nur noch zu zeigen, dass \(H_a\) auf dem Umkreis (grün) des \(\triangle HCH_b\) liegt. Schaffst Du das alleine? Tipp: Thaleskreis; die Winkel bei \(H_a\) und \(H_b\) sind rechte.
Damit sollte gezeigt sein, dass \(P\), \(Q\) und \(R\) auf einer (der simsonschen) Geraden liegen. Mache das gleiche für \(\triangle BHH_c\), damit liegen auch die Punkte \(Q\), \(R\) und \(S\) auf einer Geraden. Da es sich in jedem Fall um die Gerade durch \(Q\) und \(R\) handelt, liegen alle vier Punkte auf einer Geraden.
Falls noch etwas unklar ist, so melde Dich bitte.
Gruß Werner