Aloha :)
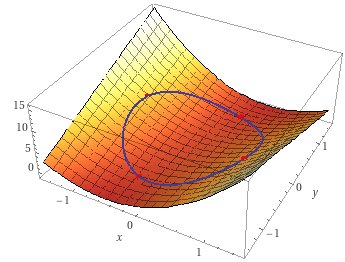
Du schaust zuerst, ob die Funktion$$f(x;y)=4x^2-3xy$$ohne die Nebenbedingung ein Exremum hat, das vielleicht zufällig im Kreis \(K\) liegt:$$K=\{(x;y)\in\mathbb R^2\,\big|\,x^2+y^2\le1\}$$
Die möglichen Kandidaten dazu findest du dort, wo der Gradient verschwindet:$$\binom{0}{0}\stackrel!=\operatorname{grad}f(x;y)=\binom{8x-3y}{-3x}\implies x=0\implies y=0$$
Wir prüfen den einzigen Kandidaten \((0|0)\) mit Hilfe der Hesse-Matrix:$$H(x;y)=\left(\begin{array}{rr}8 & -3\\-3 & 0\end{array}\right)$$Ihre Hauptminoren sind \(8\) und \((-9)\). Daher ist die Matrix indefinit und bei \((0|0)\) liegt kein Extremum vor.
Nun können Extrema noch auf dem Rand der Kreisscheibe liegen. Um das zu prüfen, müssen wir die Funktion \(f(x;y)\) unter einer konstanten Nebenbedingung \(g(x;y)\) optimieren:$$f(x;y)=4x^2-3xy\quad;\quad g(x;y)=x^2+y^2=1$$
Nach Lagrange finden wir Kandidaten-Punkte dort, wo der Gradient der zu optimierenden Funktion eine Linearkombination der Gradienten aller Nebenbedingungen ist:$$\operatorname{grad}f(x;y)\stackrel!=\lambda\operatorname{grad}g(x;y)\implies\binom{8x-3y}{-3x}\stackrel!=\lambda\binom{2x}{2y}$$Beide Gradienten müssen offenbar parallel oder antiparallel zueinander orientiert sein. Daher spannen sie keine Fläche auf und ihre gemeinsame Determinante verschwindet:$$0\stackrel!=\left|\begin{array}{rr}8x-3y & 2x\\-3x & 2y\end{array}\right|=16xy-6y^2+6x^2=2(3x-y)(x+3y)\implies$$$$y=3x\quad\lor\quad x=-3y$$
Wir setzen beide Lagrange-Forderungen in die Nebenbedingung ein:$$y=3x\implies 1=x^2+(3x)^2=10x^2\implies x=\frac{\pm1}{\sqrt{10}}\implies y=\frac{\pm3}{\sqrt{10}}$$$$x=-3y\implies 1=(-3y)^2+y^2=10y^2\implies y=\frac{\pm1}{\sqrt{10}}\implies x=\frac{\mp3}{\sqrt{10}}$$
Damit haben wir 4 Kandidaten für Exrema gefunden:$$\red{K_1\left(\frac{1}{\sqrt{10}}\bigg|\frac{3}{\sqrt{10}}\right)}\quad;\quad \red{K_2\left(\frac{-1}{\sqrt{10}}\bigg|\frac{-3}{\sqrt{10}}\right)}\quad;\quad \green{K_3\left(\frac{3}{\sqrt{10}}\bigg|\frac{-1}{\sqrt{10}}\right)}\quad;\quad \green{K_4\left(\frac{-3}{\sqrt{10}}\bigg|\frac{1}{\sqrt{10}}\right)}$$
Wegen \(\left(f(\vec k_1)=f(\vec k_2)=-\frac12\right)\) und \(\left(f(\vec k_3)=f(\vec k_4)=+\frac92\right)\) sind die ersten beiden Kandidaten globale Minima und die beiden letzten Kandidaten gloable Maxima auf dem Kreisrand.