Bestimme den Wert für k, bei dem der Hochpunkt der Funktionschar den minimalsten Abstand zu dem Punkt (0|2) hat.

Question

Aufgabe:

… Bestimme den Wert für k, bei dem der Hochpunkt der Funktionsschar k²-kx³ den minimalsten Abstand zu dem Punkt (0|2) hat.

Der Hochpunkt liegt bei $$\left(\frac{2}{3\cdot k}|\frac{4}{27\cdot k^2}\right)$$

Problem/Ansatz:

… Bekommen für k keinen Wert raus.

Ansatz:

Abstand 2 Punkte:

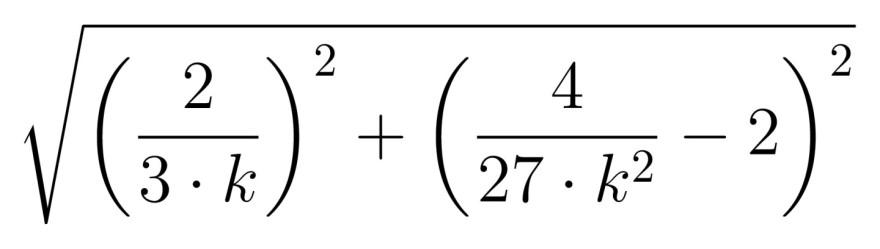
Klammern auflösen:

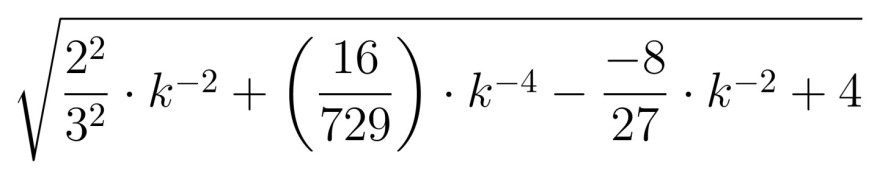
Ableitung bilden und den Nenner vernachlässigen:

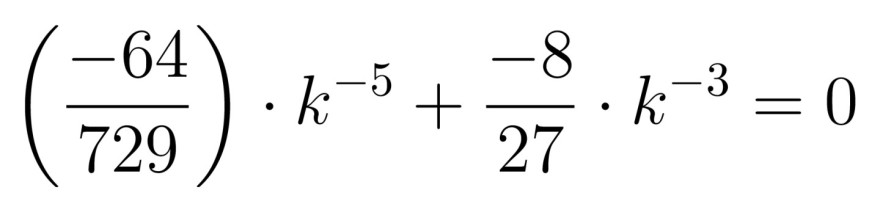
k^-3 ausklammern

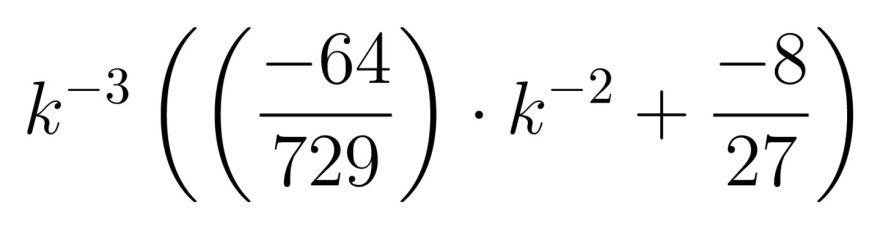
Satz vom Nullprodukt, dreifache Nullstelle bei k = 0, ! aber bei k = 0 gibt es keinen Hochpunkt.

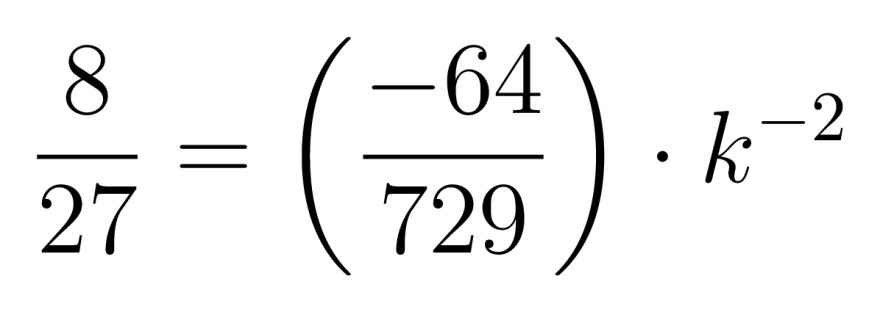
Und das bekomme ich leider nicht nach k aufgelöst.

Wo liegt also der Fehler @döschwo ?

Comments

den minimalsten Abstand

"minimal" ist bereits ein Superlativ !

Wieso ist der Hochpunkt $\left(\frac{2}{3\cdot k}|\frac{4}{27\cdot k^2}\right)$?

Ich fürchte, ich habe die Aufgabe nicht verstanden !

Answer 1

d² = (2/(3·k) - 0)² + (4/(27·k²) - 2)²

d² = - 4/(27·k²) + 16/(729·k⁴) + 4

(d²)' = 8/(27·k³) - 64/(729·k⁵) = 0 --> k = ± 2/9·√6

Comments

Das haut hin, vielen Dank!

---

Ah. Da lag dein Fehler. Die Funktion lautet

f(x) = x² - k*x³ und nicht wie oben von dir falsch angegeben.

---

f(x) = x2 - k*x3 und nicht wie oben von dir falsch angegeben.

Inwiefern soll ein k statt x in der Funktionsgleichung was an der Rechnung ändern? Mit "Fehler" meinte ich hier nicht irgendeinen unrelevanten Flüchtigkeitsfehler, sondern welchen relevanten Rechenfehler ich begangen habe.

Der Fehler ist, ich komme auf 4/27, während du auf -4/27 kommst.

An dieser Stelle habe ich den ersten Bruch von k^(-2) auf 12/27 erweitert und davon dann 8/27 abgezogen. (12-8= +4)

Wie kommst du auf -4/27?

---

Wie kommst du auf -4/27?

Nimm mal ein Rechentool wie Photomath um dir den Term vereinfachen zu lassen. Alternativ kann auch ein CAS helfen. Dann musst du das aber Schrittweise eingeben.

---

Hast du an die binomische Formel gedacht?

---

Hast du an die binomische Formel gedacht?

Ja die zweite binomische Formel: (a-b)² = a² - 2ab + b²

aus:

wird

ach ne Minus 16

---

ach ne Minus 16

Na. Dann sollte das ja jetzt klar sein denke ich.

Answer 2

Rechne jetzt beide Seiten mal 729k².

Comments

Aus negativen Zahlen kann man nicht die Wurzel ziehen!

---

Du solltest davon ausgehen, dass dem Antwortgeber das, was Du meinst, durchaus bekannt ist.