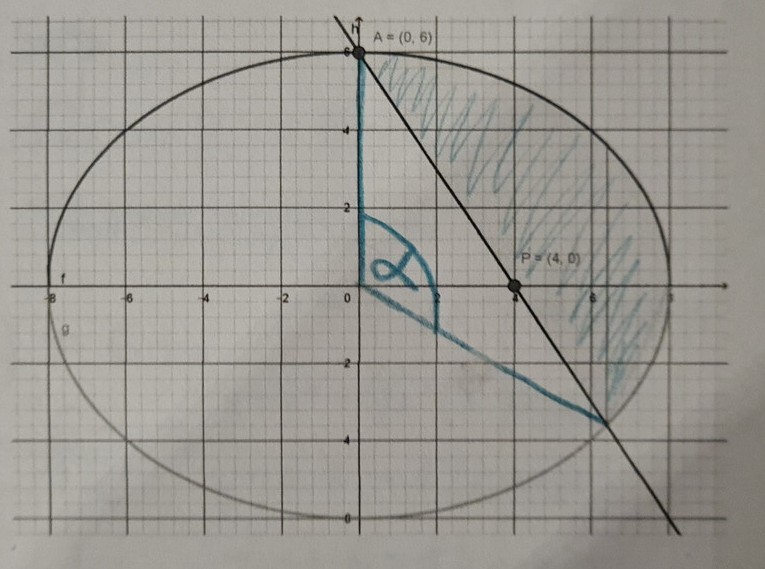
Wie berechnet man den markierten Flächeninhalt und den Winkel Alpha?
Gegeben ist: a = 8, b = 6, r = 8, k = 6/8,
Geradengleichung: y = - 1,5x + 6
Meine Frage wäre wie ich den Winkel berechnen, und in die allgemeine Gleichung für den Flächeninhalt eines Ellipsenabschnitts einsetzen kann.
Vielen Dank im voraus.
Link zum Bild: